Learning Markov networks with context-specific independences
Paper and Code
Jul 15, 2013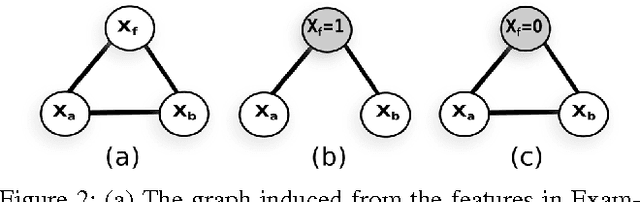

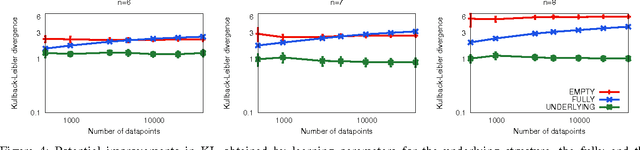
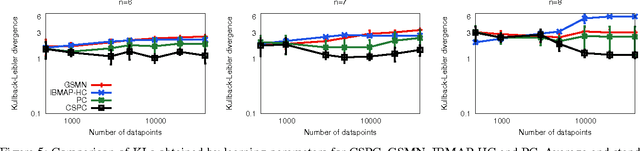
Learning the Markov network structure from data is a problem that has received considerable attention in machine learning, and in many other application fields. This work focuses on a particular approach for this purpose called independence-based learning. Such approach guarantees the learning of the correct structure efficiently, whenever data is sufficient for representing the underlying distribution. However, an important issue of such approach is that the learned structures are encoded in an undirected graph. The problem with graphs is that they cannot encode some types of independence relations, such as the context-specific independences. They are a particular case of conditional independences that is true only for a certain assignment of its conditioning set, in contrast to conditional independences that must hold for all its assignments. In this work we present CSPC, an independence-based algorithm for learning structures that encode context-specific independences, and encoding them in a log-linear model, instead of a graph. The central idea of CSPC is combining the theoretical guarantees provided by the independence-based approach with the benefits of representing complex structures by using features in a log-linear model. We present experiments in a synthetic case, showing that CSPC is more accurate than the state-of-the-art IB algorithms when the underlying distribution contains CSIs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge