Efficient Independence-Based MAP Approach for Robust Markov Networks Structure Discovery
Paper and Code
Jan 18, 2011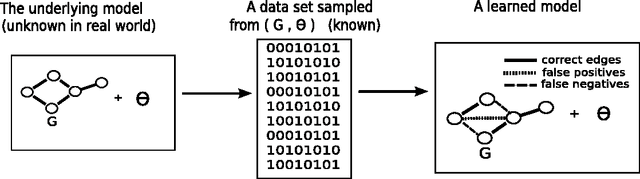
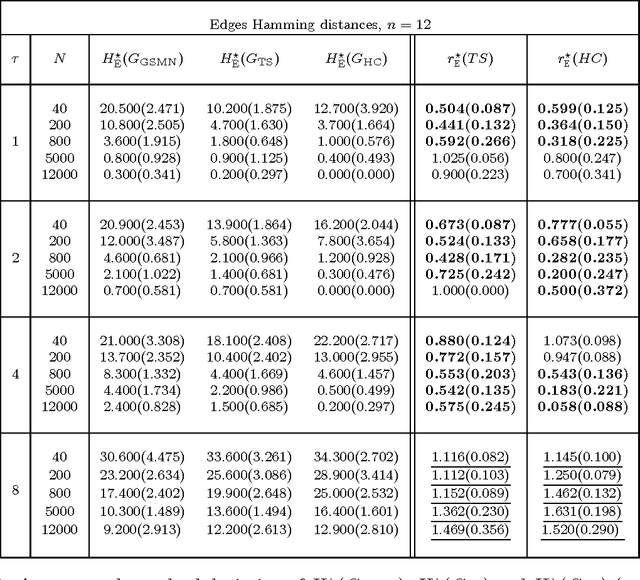
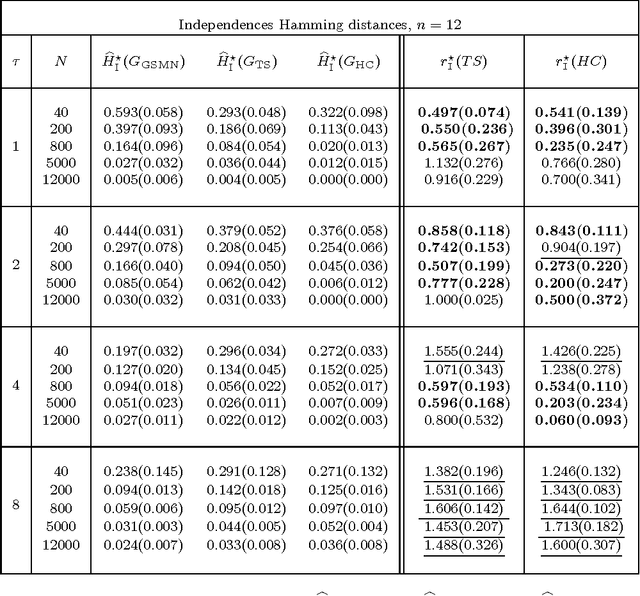
This work introduces the IB-score, a family of independence-based score functions for robust learning of Markov networks independence structures. Markov networks are a widely used graphical representation of probability distributions, with many applications in several fields of science. The main advantage of the IB-score is the possibility of computing it without the need of estimation of the numerical parameters, an NP-hard problem, usually solved through an approximate, data-intensive, iterative optimization. We derive a formal expression for the IB-score from first principles, mainly maximum a posteriori and conditional independence properties, and exemplify several instantiations of it, resulting in two novel algorithms for structure learning: IBMAP-HC and IBMAP-TS. Experimental results over both artificial and real world data show these algorithms achieve important error reductions in the learnt structures when compared with the state-of-the-art independence-based structure learning algorithm GSMN, achieving increments of more than 50% in the amount of independencies they encode correctly, and in some cases, learning correctly over 90% of the edges that GSMN learnt incorrectly. Theoretical analysis shows IBMAP-HC proceeds efficiently, achieving these improvements in a time polynomial to the number of random variables in the domain.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge