Blankets Joint Posterior score for learning Markov network structures

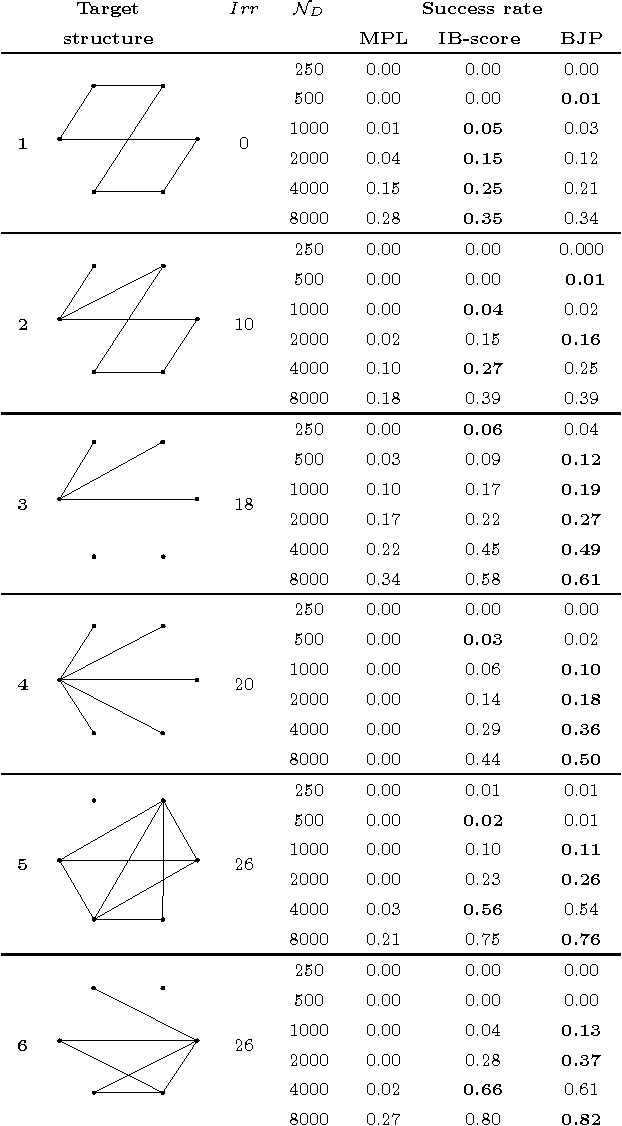
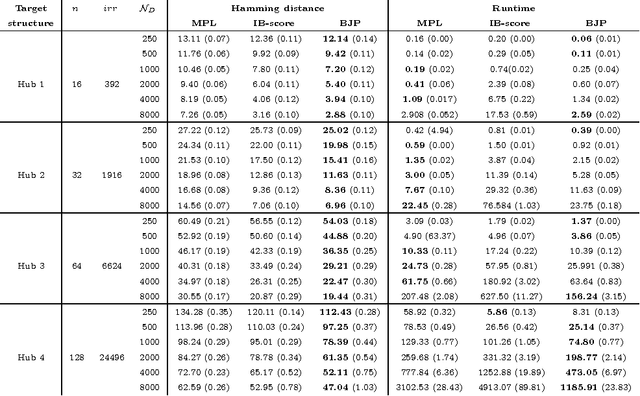
Markov networks are extensively used to model complex sequential, spatial, and relational interactions in a wide range of fields. By learning the structure of independences of a domain, more accurate joint probability distributions can be obtained for inference tasks or, more directly, for interpreting the most significant relations among the variables. Recently, several researchers have investigated techniques for automatically learning the structure from data by obtaining the probabilistic maximum-a-posteriori structure given the available data. However, all the approximations proposed decompose the posterior of the whole structure into local sub-problems, by assuming that the posteriors of the Markov blankets of all the variables are mutually independent. In this work, we propose a scoring function for relaxing such assumption. The Blankets Joint Posterior score computes the joint posterior of structures as a joint distribution of the collection of its Markov blankets. Essentially, the whole posterior is obtained by computing the posterior of the blanket of each variable as a conditional distribution that takes into account information from other blankets in the network. We show in our experimental results that the proposed approximation can improve the sample complexity of state-of-the-art scores when learning complex networks, where the independence assumption between blanket variables is clearly incorrect.

The Grow-Shrink strategy for learning Markov network structures constrained by context-specific independences

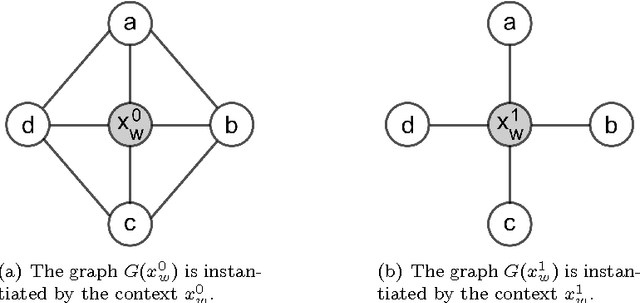
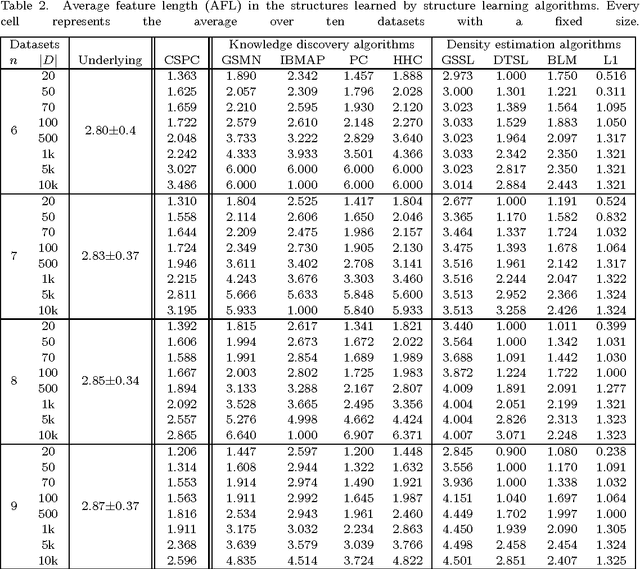
Markov networks are models for compactly representing complex probability distributions. They are composed by a structure and a set of numerical weights. The structure qualitatively describes independences in the distribution, which can be exploited to factorize the distribution into a set of compact functions. A key application for learning structures from data is to automatically discover knowledge. In practice, structure learning algorithms focused on "knowledge discovery" present a limitation: they use a coarse-grained representation of the structure. As a result, this representation cannot describe context-specific independences. Very recently, an algorithm called CSPC was designed to overcome this limitation, but it has a high computational complexity. This work tries to mitigate this downside presenting CSGS, an algorithm that uses the Grow-Shrink strategy for reducing unnecessary computations. On an empirical evaluation, the structures learned by CSGS achieve competitive accuracies and lower computational complexity with respect to those obtained by CSPC.