A survey on independence-based Markov networks learning
Paper and Code
Nov 20, 2013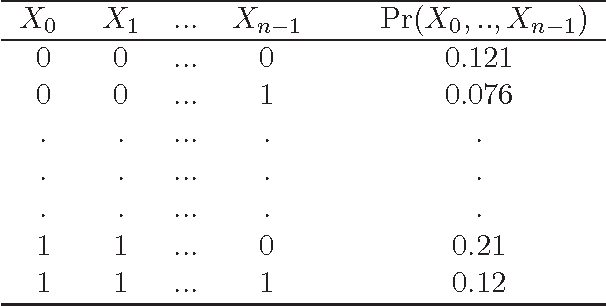
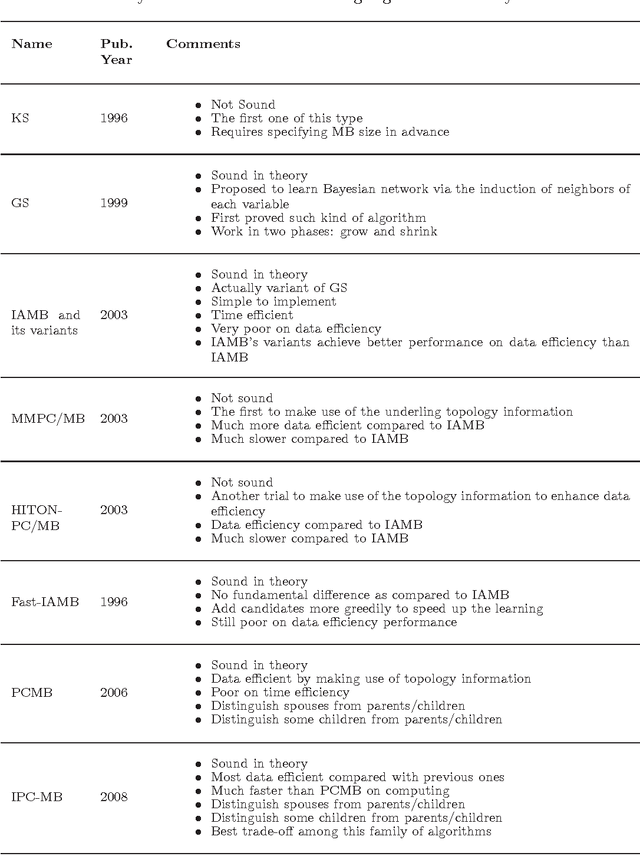
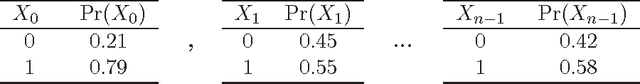
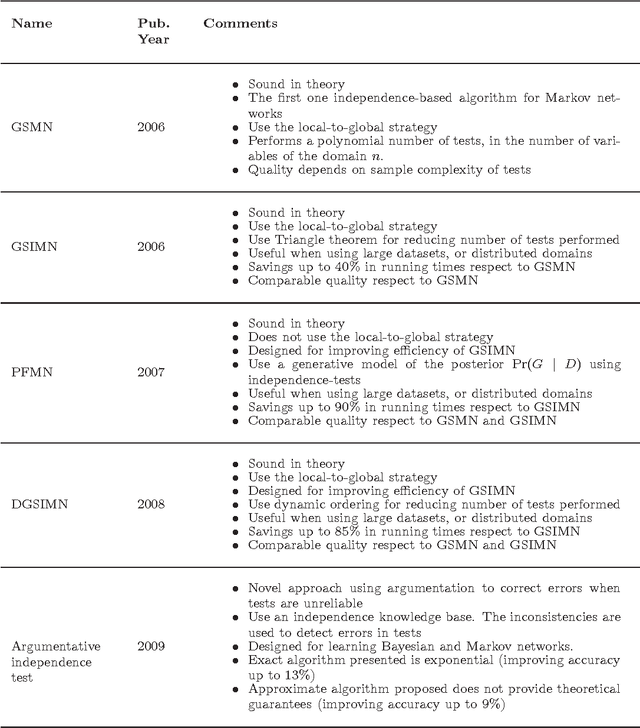
This work reports the most relevant technical aspects in the problem of learning the \emph{Markov network structure} from data. Such problem has become increasingly important in machine learning, and many other application fields of machine learning. Markov networks, together with Bayesian networks, are probabilistic graphical models, a widely used formalism for handling probability distributions in intelligent systems. Learning graphical models from data have been extensively applied for the case of Bayesian networks, but for Markov networks learning it is not tractable in practice. However, this situation is changing with time, given the exponential growth of computers capacity, the plethora of available digital data, and the researching on new learning technologies. This work stresses on a technology called independence-based learning, which allows the learning of the independence structure of those networks from data in an efficient and sound manner, whenever the dataset is sufficiently large, and data is a representative sampling of the target distribution. In the analysis of such technology, this work surveys the current state-of-the-art algorithms for learning Markov networks structure, discussing its current limitations, and proposing a series of open problems where future works may produce some advances in the area in terms of quality and efficiency. The paper concludes by opening a discussion about how to develop a general formalism for improving the quality of the structures learned, when data is scarce.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge