Learning Partially Observable Deterministic Action Models

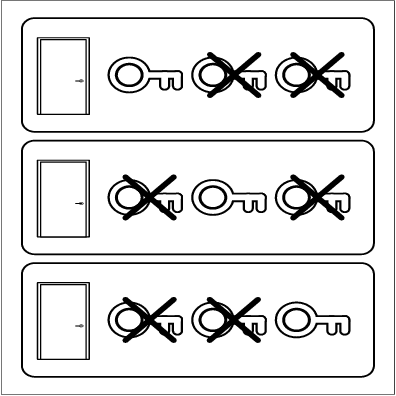
We present exact algorithms for identifying deterministic-actions effects and preconditions in dynamic partially observable domains. They apply when one does not know the action model(the way actions affect the world) of a domain and must learn it from partial observations over time. Such scenarios are common in real world applications. They are challenging for AI tasks because traditional domain structures that underly tractability (e.g., conditional independence) fail there (e.g., world features become correlated). Our work departs from traditional assumptions about partial observations and action models. In particular, it focuses on problems in which actions are deterministic of simple logical structure and observation models have all features observed with some frequency. We yield tractable algorithms for the modified problem for such domains. Our algorithms take sequences of partial observations over time as input, and output deterministic action models that could have lead to those observations. The algorithms output all or one of those models (depending on our choice), and are exact in that no model is misclassified given the observations. Our algorithms take polynomial time in the number of time steps and state features for some traditional action classes examined in the AI-planning literature, e.g., STRIPS actions. In contrast, traditional approaches for HMMs and Reinforcement Learning are inexact and exponentially intractable for such domains. Our experiments verify the theoretical tractability guarantees, and show that we identify action models exactly. Several applications in planning, autonomous exploration, and adventure-game playing already use these results. They are also promising for probabilistic settings, partially observable reinforcement learning, and diagnosis.

Efficient Approximation for Triangulation of Minimum Treewidth

We present four novel approximation algorithms for finding triangulation of minimum treewidth. Two of the algorithms improve on the running times of algorithms by Robertson and Seymour, and Becker and Geiger that approximate the optimum by factors of 4 and 3 2/3, respectively. A third algorithm is faster than those but gives an approximation factor of 4 1/2. The last algorithm is yet faster, producing factor-O(lg/k) approximations in polynomial time. Finding triangulations of minimum treewidth for graphs is central to many problems in computer science. Real-world problems in artificial intelligence, VLSI design and databases are efficiently solvable if we have an efficient approximation algorithm for them. We report on experimental results confirming the effectiveness of our algorithms for large graphs associated with real-world problems.

Lifted Relational Variational Inference

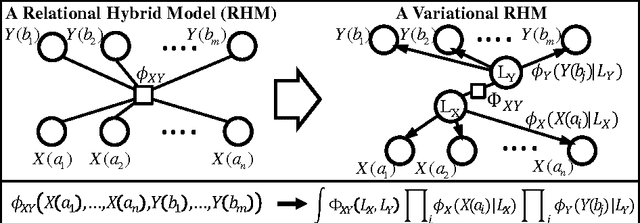
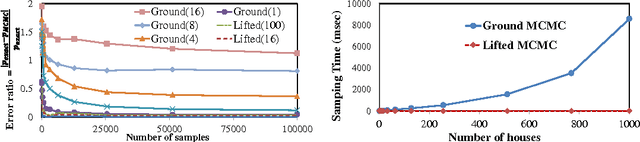
Hybrid continuous-discrete models naturally represent many real-world applications in robotics, finance, and environmental engineering. Inference with large-scale models is challenging because relational structures deteriorate rapidly during inference with observations. The main contribution of this paper is an efficient relational variational inference algorithm that factors largescale probability models into simpler variational models, composed of mixtures of iid (Bernoulli) random variables. The algorithm takes probability relational models of largescale hybrid systems and converts them to a close-to-optimal variational models. Then, it efficiently calculates marginal probabilities on the variational models by using a latent (or lifted) variable elimination or a lifted stochastic sampling. This inference is unique because it maintains the relational structure upon individual observations and during inference steps.

Reachability Under Uncertainty

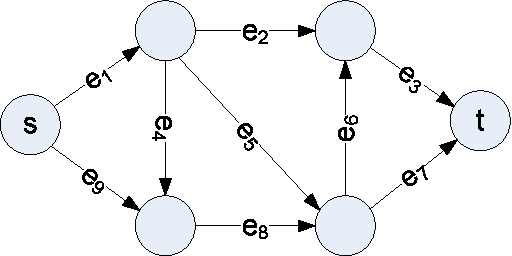
In this paper we introduce a new network reachability problem where the goal is to find the most reliable path between two nodes in a network, represented as a directed acyclic graph. Individual edges within this network may fail according to certain probabilities, and these failure probabilities may depend on the values of one or more hidden variables. This problem may be viewed as a generalization of shortest-path problems for finding minimum cost paths or Viterbi-type problems for finding highest-probability sequences of states, where the addition of the hidden variables introduces correlations that are not handled by previous algorithms. We give theoretical results characterizing this problem including an NP-hardness proof. We also give an exact algorithm and a more efficient approximation algorithm for this problem.

Sampling First Order Logical Particles

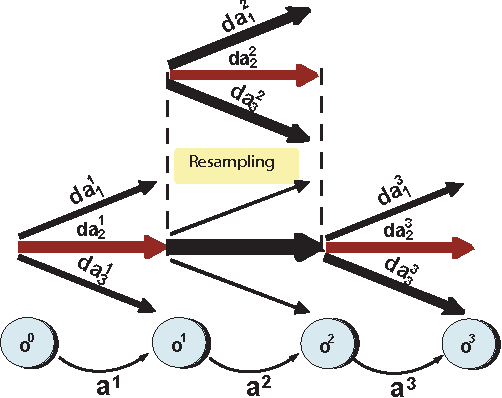
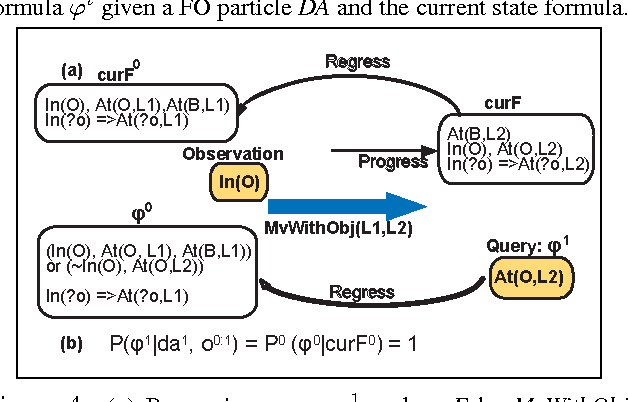
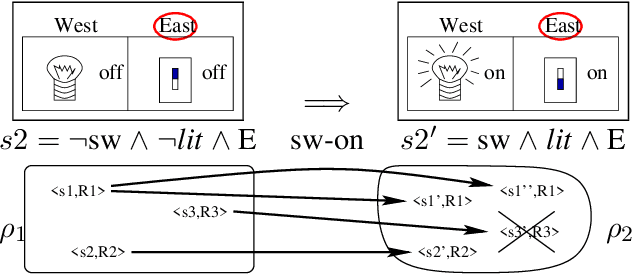
Approximate inference in dynamic systems is the problem of estimating the state of the system given a sequence of actions and partial observations. High precision estimation is fundamental in many applications like diagnosis, natural language processing, tracking, planning, and robotics. In this paper we present an algorithm that samples possible deterministic executions of a probabilistic sequence. The algorithm takes advantage of a compact representation (using first order logic) for actions and world states to improve the precision of its estimation. Theoretical and empirical results show that the algorithm's expected error is smaller than propositional sampling and Sequential Monte Carlo (SMC) sampling techniques.

Lifted Inference for Relational Continuous Models

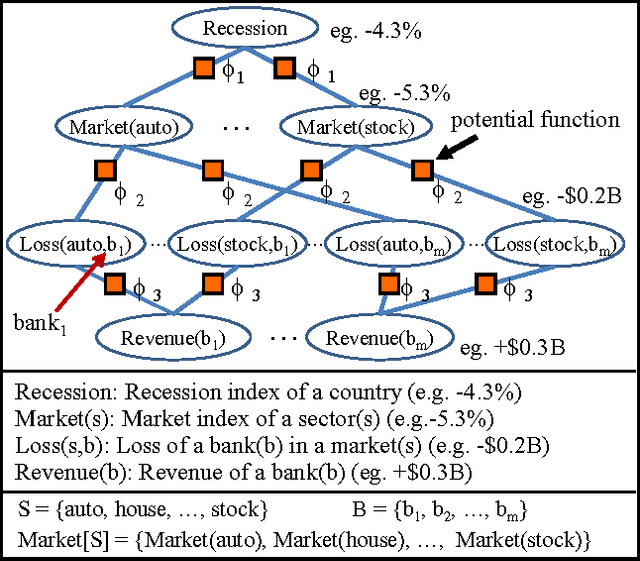
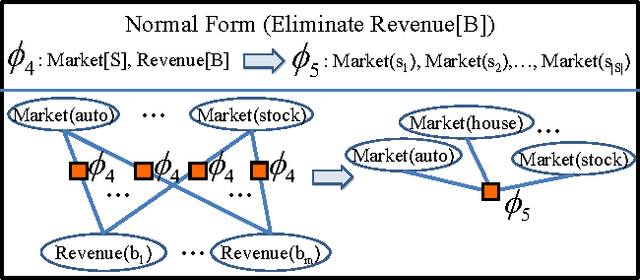
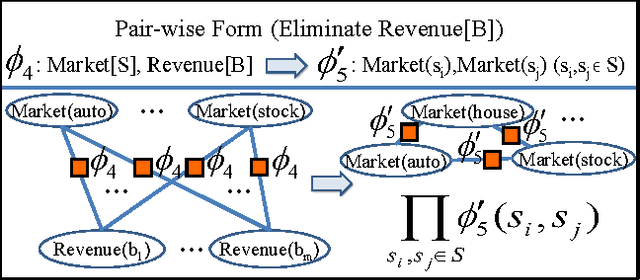
Relational Continuous Models (RCMs) represent joint probability densities over attributes of objects, when the attributes have continuous domains. With relational representations, they can model joint probability distributions over large numbers of variables compactly in a natural way. This paper presents a new exact lifted inference algorithm for RCMs, thus it scales up to large models of real world applications. The algorithm applies to Relational Pairwise Models which are (relational) products of potentials of arity 2. Our algorithm is unique in two ways. First, it substantially improves the efficiency of lifted inference with variables of continuous domains. When a relational model has Gaussian potentials, it takes only linear-time compared to cubic time of previous methods. Second, it is the first exact inference algorithm which handles RCMs in a lifted way. The algorithm is illustrated over an example from econometrics. Experimental results show that our algorithm outperforms both a groundlevel inference algorithm and an algorithm built with previously-known lifted methods.

Reasoning about RoboCup Soccer Narratives

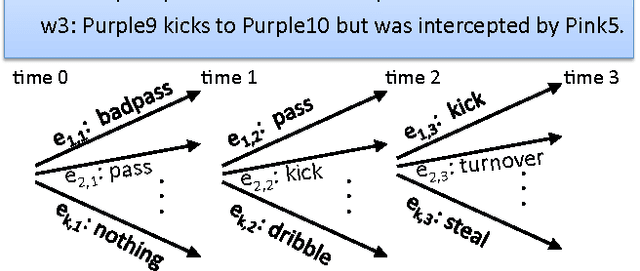
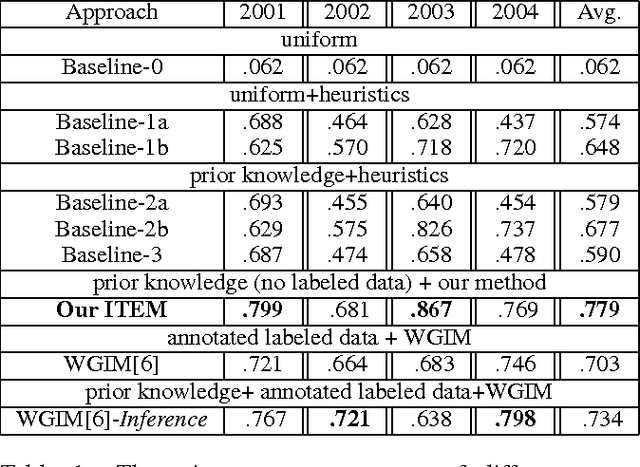
This paper presents an approach for learning to translate simple narratives, i.e., texts (sequences of sentences) describing dynamic systems, into coherent sequences of events without the need for labeled training data. Our approach incorporates domain knowledge in the form of preconditions and effects of events, and we show that it outperforms state-of-the-art supervised learning systems on the task of reconstructing RoboCup soccer games from their commentaries.

Interpolation Theorems for Nonmonotonic Reasoning Systems

Craig's interpolation theorem (Craig 1957) is an important theorem known for propositional logic and first-order logic. It says that if a logical formula $\beta$ logically follows from a formula $\alpha$, then there is a formula $\gamma$, including only symbols that appear in both $\alpha,\beta$, such that $\beta$ logically follows from $\gamma$ and $\gamma$ logically follows from $\alpha$. Such theorems are important and useful for understanding those logics in which they hold as well as for speeding up reasoning with theories in those logics. In this paper we present interpolation theorems in this spirit for three nonmonotonic systems: circumscription, default logic and logic programs with the stable models semantics (a.k.a. answer set semantics). These results give us better understanding of those logics, especially in contrast to their nonmonotonic characteristics. They suggest that some \emph{monotonicity} principle holds despite the failure of classic monotonicity for these logics. Also, they sometimes allow us to use methods for the decomposition of reasoning for these systems, possibly increasing their applicability and tractability. Finally, they allow us to build structured representations that use those logics.