Reachability Under Uncertainty
Paper and Code
Jun 20, 2012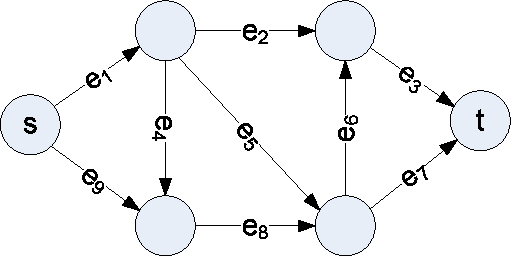
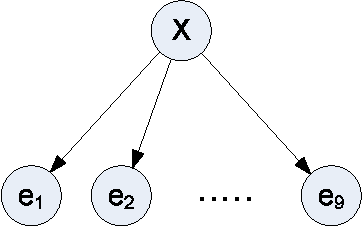
In this paper we introduce a new network reachability problem where the goal is to find the most reliable path between two nodes in a network, represented as a directed acyclic graph. Individual edges within this network may fail according to certain probabilities, and these failure probabilities may depend on the values of one or more hidden variables. This problem may be viewed as a generalization of shortest-path problems for finding minimum cost paths or Viterbi-type problems for finding highest-probability sequences of states, where the addition of the hidden variables introduces correlations that are not handled by previous algorithms. We give theoretical results characterizing this problem including an NP-hardness proof. We also give an exact algorithm and a more efficient approximation algorithm for this problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge