Lifted Inference for Relational Continuous Models
Paper and Code
Mar 15, 2012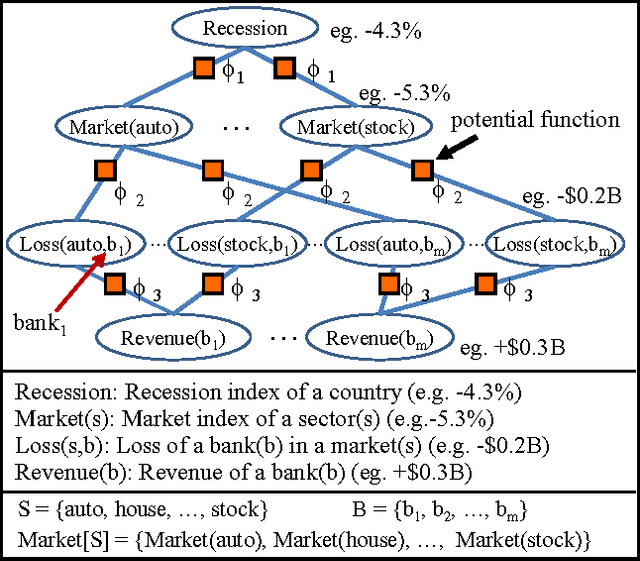

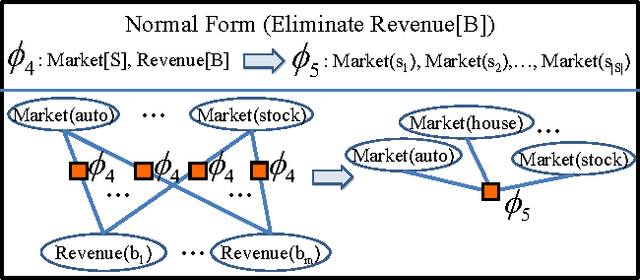
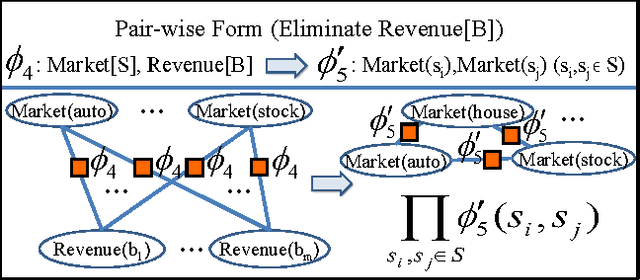
Relational Continuous Models (RCMs) represent joint probability densities over attributes of objects, when the attributes have continuous domains. With relational representations, they can model joint probability distributions over large numbers of variables compactly in a natural way. This paper presents a new exact lifted inference algorithm for RCMs, thus it scales up to large models of real world applications. The algorithm applies to Relational Pairwise Models which are (relational) products of potentials of arity 2. Our algorithm is unique in two ways. First, it substantially improves the efficiency of lifted inference with variables of continuous domains. When a relational model has Gaussian potentials, it takes only linear-time compared to cubic time of previous methods. Second, it is the first exact inference algorithm which handles RCMs in a lifted way. The algorithm is illustrated over an example from econometrics. Experimental results show that our algorithm outperforms both a groundlevel inference algorithm and an algorithm built with previously-known lifted methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge