Sampling First Order Logical Particles
Paper and Code
Jun 13, 2012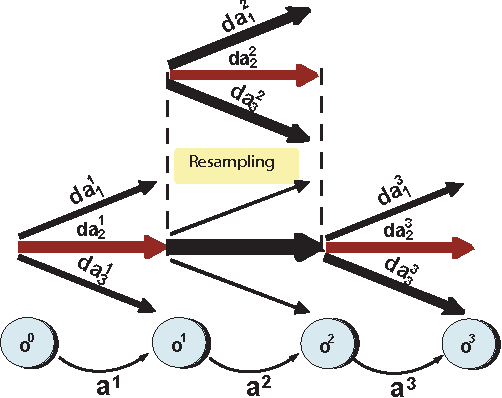

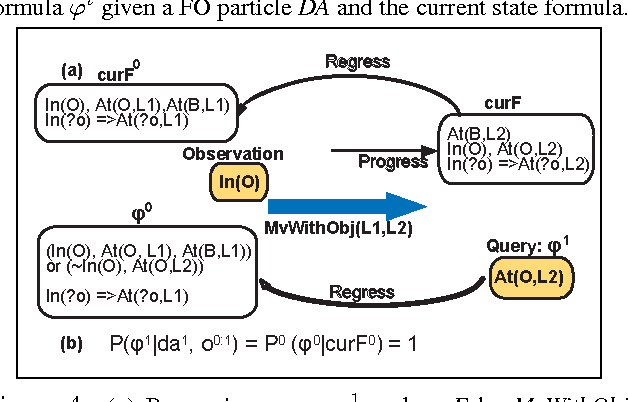

Approximate inference in dynamic systems is the problem of estimating the state of the system given a sequence of actions and partial observations. High precision estimation is fundamental in many applications like diagnosis, natural language processing, tracking, planning, and robotics. In this paper we present an algorithm that samples possible deterministic executions of a probabilistic sequence. The algorithm takes advantage of a compact representation (using first order logic) for actions and world states to improve the precision of its estimation. Theoretical and empirical results show that the algorithm's expected error is smaller than propositional sampling and Sequential Monte Carlo (SMC) sampling techniques.
* Appears in Proceedings of the Twenty-Fourth Conference on Uncertainty
in Artificial Intelligence (UAI2008)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge