${\tt MORALS}$: Analysis of High-Dimensional Robot Controllers via Topological Tools in a Latent Space

Estimating the region of attraction (${\tt RoA}$) for a robotic system's controller is essential for safe application and controller composition. Many existing methods require access to a closed-form expression that limit applicability to data-driven controllers. Methods that operate only over trajectory rollouts tend to be data-hungry. In prior work, we have demonstrated that topological tools based on Morse Graphs offer data-efficient ${\tt RoA}$ estimation without needing an analytical model. They struggle, however, with high-dimensional systems as they operate over a discretization of the state space. This paper presents ${\it Mo}$rse Graph-aided discovery of ${\it R}$egions of ${\it A}$ttraction in a learned ${\it L}$atent ${\it S}$pace (${\tt MORALS}$). The approach combines autoencoding neural networks with Morse Graphs. ${\tt MORALS}$ shows promising predictive capabilities in estimating attractors and their ${\tt RoA}$s for data-driven controllers operating over high-dimensional systems, including a 67-dim humanoid robot and a 96-dim 3-fingered manipulator. It first projects the dynamics of the controlled system into a learned latent space. Then, it constructs a reduced form of Morse Graphs representing the bistability of the underlying dynamics, i.e., detecting when the controller results in a desired versus an undesired behavior. The evaluation on high-dimensional robotic datasets indicates the data efficiency of the approach in ${\tt RoA}$ estimation.

Data-Efficient Characterization of the Global Dynamics of Robot Controllers with Confidence Guarantees

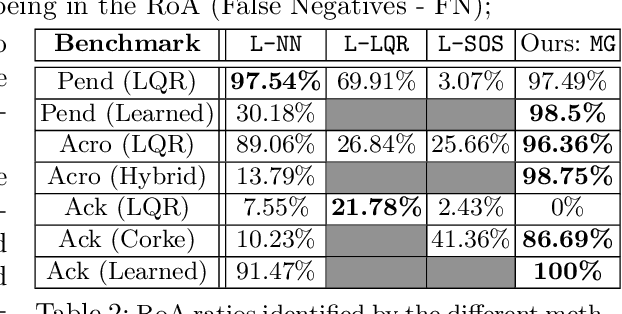
This paper proposes an integration of surrogate modeling and topology to significantly reduce the amount of data required to describe the underlying global dynamics of robot controllers, including closed-box ones. A Gaussian Process (GP), trained with randomized short trajectories over the state-space, acts as a surrogate model for the underlying dynamical system. Then, a combinatorial representation is built and used to describe the dynamics in the form of a directed acyclic graph, known as {\it Morse graph}. The Morse graph is able to describe the system's attractors and their corresponding regions of attraction (\roa). Furthermore, a pointwise confidence level of the global dynamics estimation over the entire state space is provided. In contrast to alternatives, the framework does not require estimation of Lyapunov functions, alleviating the need for high prediction accuracy of the GP. The framework is suitable for data-driven controllers that do not expose an analytical model as long as Lipschitz-continuity is satisfied. The method is compared against established analytical and recent machine learning alternatives for estimating \roa s, outperforming them in data efficiency without sacrificing accuracy. Link to code: https://go.rutgers.edu/49hy35en

Persistent Homology Guided Monte-Carlo Tree Search for Effective Non-Prehensile Manipulation

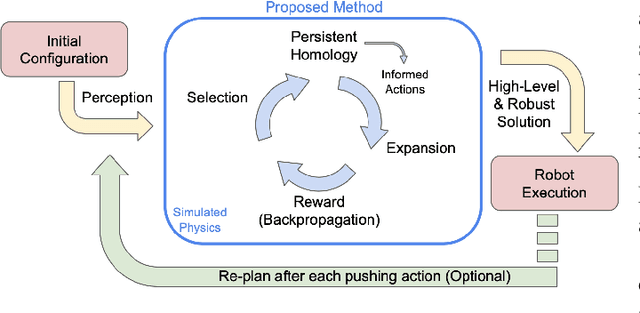
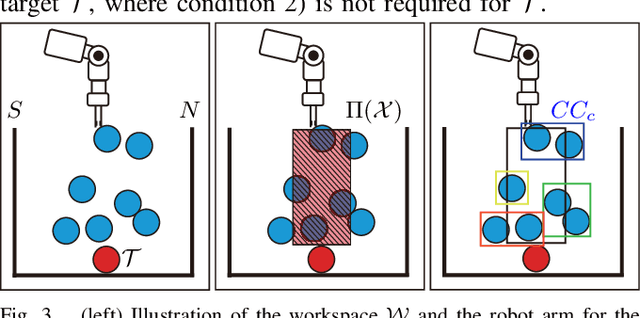
Performing object retrieval tasks in messy real-world workspaces involves the challenges of \emph{uncertainty} and \emph{clutter}. One option is to solve retrieval problems via a sequence of prehensile pick-n-place operations, which can be computationally expensive to compute in highly-cluttered scenarios and also inefficient to execute. The proposed framework selects the option of performing non-prehensile actions, such as pushing, to clean a cluttered workspace to allow a robotic arm to retrieve a target object. Non-prehensile actions, allow to interact simultaneously with multiple objects, which can speed up execution. At the same time, they can significantly increase uncertainty as it is not easy to accurately estimate the outcome of a pushing operation in clutter. The proposed framework integrates topological tools and Monte-Carlo tree search to achieve effective and robust pushing for object retrieval problems. In particular, it proposes using persistent homology to automatically identify manageable clustering of blocking objects in the workspace without the need for manually adjusting hyper-parameters. Furthermore, MCTS uses this information to explore feasible actions to push groups of objects together, aiming to minimize the number of pushing actions needed to clear the path to the target object. Real-world experiments using a Baxter robot, which involves some noise in actuation, show that the proposed framework achieves a higher success rate in solving retrieval tasks in dense clutter compared to state-of-the-art alternatives. Moreover, it produces high-quality solutions with a small number of pushing actions improving the overall execution time. More critically, it is robust enough that it allows to plan the sequence of actions offline and then execute them reliably online with Baxter.

Morse Graphs: Topological Tools for Analyzing the Global Dynamics of Robot Controllers

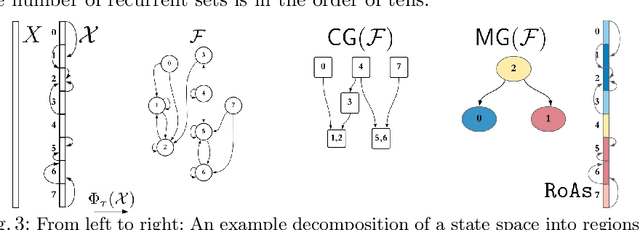
Understanding the global dynamics of a robot controller, such as identifying attractors and their regions of attraction (RoA), is important for safe deployment and synthesizing more effective hybrid controllers. This paper proposes a topological framework to analyze the global dynamics of robot controllers, even data-driven ones, in an effective and explainable way. It builds a combinatorial representation representing the underlying system's state space and non-linear dynamics, which is summarized in a directed acyclic graph, the Morse graph. The approach only probes the dynamics locally by forward propagating short trajectories over a state-space discretization, which needs to be a Lipschitz-continuous function. The framework is evaluated given either numerical or data-driven controllers for classical robotic benchmarks. It is compared against established analytical and recent machine learning alternatives for estimating the RoAs of such controllers. It is shown to outperform them in accuracy and efficiency. It also provides deeper insights as it describes the global dynamics up to the discretization's resolution. This allows to use the Morse graph to identify how to synthesize controllers to form improved hybrid solutions or how to identify the physical limitations of a robotic system.

Persistent Homology for Effective Non-Prehensile Manipulation

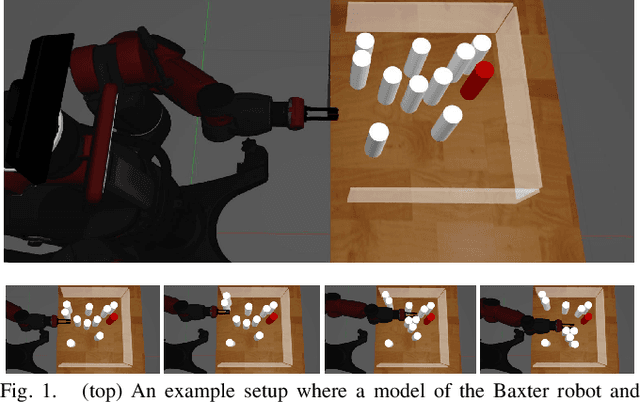
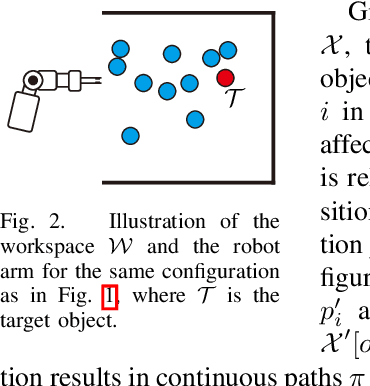
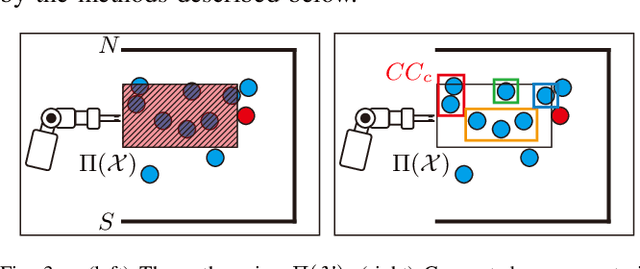
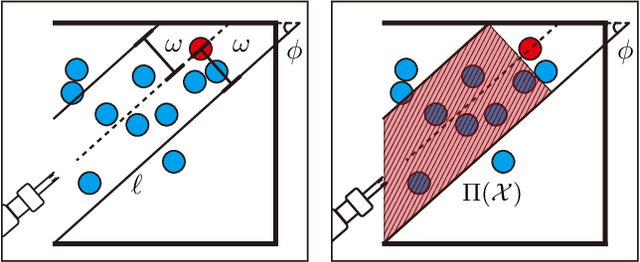
This work explores the use of topological tools for achieving effective non-prehensile manipulation in cluttered, constrained workspaces. In particular, it proposes the use of persistent homology as a guiding principle in identifying the appropriate non-prehensile actions, such as pushing, to clean a cluttered space with a robotic arm so as to allow the retrieval of a target object. Persistent homology enables the automatic identification of connected components of blocking objects in the space without the need for manual input or tuning of parameters. The proposed algorithm uses this information to push groups of cylindrical objects together and aims to minimize the number of pushing actions needed to reach to the target. Simulated experiments in a physics engine using a model of the Baxter robot show that the proposed topology-driven solution is achieving significantly higher success rate in solving such constrained problems relatively to state-of-the-art alternatives from the literature. It manages to keep the number of pushing actions low, is computationally efficient and the resulting decisions and motion appear natural for effectively solving such tasks.