Data-Efficient Characterization of the Global Dynamics of Robot Controllers with Confidence Guarantees

This paper proposes an integration of surrogate modeling and topology to significantly reduce the amount of data required to describe the underlying global dynamics of robot controllers, including closed-box ones. A Gaussian Process (GP), trained with randomized short trajectories over the state-space, acts as a surrogate model for the underlying dynamical system. Then, a combinatorial representation is built and used to describe the dynamics in the form of a directed acyclic graph, known as {\it Morse graph}. The Morse graph is able to describe the system's attractors and their corresponding regions of attraction (\roa). Furthermore, a pointwise confidence level of the global dynamics estimation over the entire state space is provided. In contrast to alternatives, the framework does not require estimation of Lyapunov functions, alleviating the need for high prediction accuracy of the GP. The framework is suitable for data-driven controllers that do not expose an analytical model as long as Lipschitz-continuity is satisfied. The method is compared against established analytical and recent machine learning alternatives for estimating \roa s, outperforming them in data efficiency without sacrificing accuracy. Link to code: https://go.rutgers.edu/49hy35en

Morse Graphs: Topological Tools for Analyzing the Global Dynamics of Robot Controllers

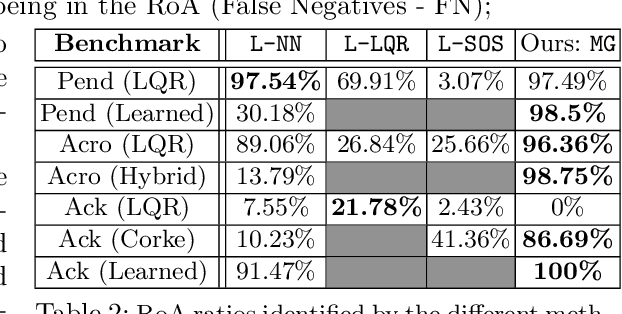
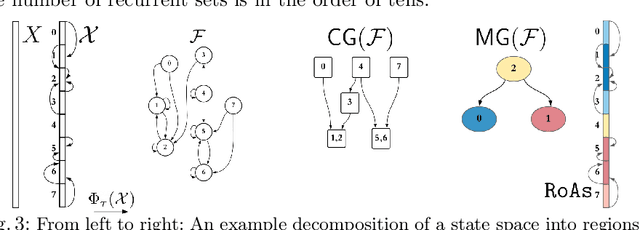
Understanding the global dynamics of a robot controller, such as identifying attractors and their regions of attraction (RoA), is important for safe deployment and synthesizing more effective hybrid controllers. This paper proposes a topological framework to analyze the global dynamics of robot controllers, even data-driven ones, in an effective and explainable way. It builds a combinatorial representation representing the underlying system's state space and non-linear dynamics, which is summarized in a directed acyclic graph, the Morse graph. The approach only probes the dynamics locally by forward propagating short trajectories over a state-space discretization, which needs to be a Lipschitz-continuous function. The framework is evaluated given either numerical or data-driven controllers for classical robotic benchmarks. It is compared against established analytical and recent machine learning alternatives for estimating the RoAs of such controllers. It is shown to outperform them in accuracy and efficiency. It also provides deeper insights as it describes the global dynamics up to the discretization's resolution. This allows to use the Morse graph to identify how to synthesize controllers to form improved hybrid solutions or how to identify the physical limitations of a robotic system.

Extracting Global Dynamics of Loss Landscape in Deep Learning Models

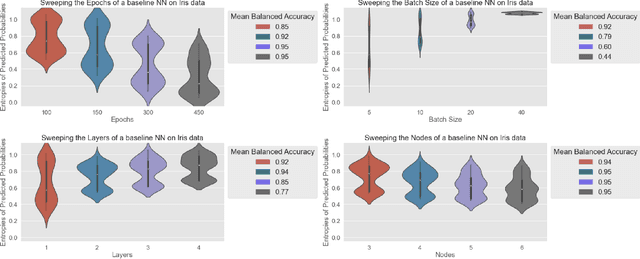
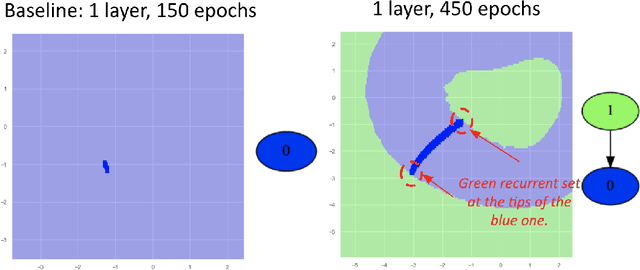
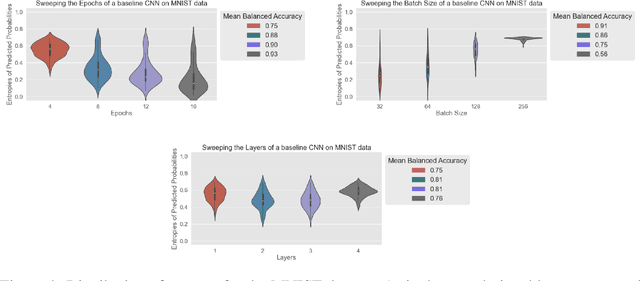
Deep learning models evolve through training to learn the manifold in which the data exists to satisfy an objective. It is well known that evolution leads to different final states which produce inconsistent predictions of the same test data points. This calls for techniques to be able to empirically quantify the difference in the trajectories and highlight problematic regions. While much focus is placed on discovering what models learn, the question of how a model learns is less studied beyond theoretical landscape characterizations and local geometric approximations near optimal conditions. Here, we present a toolkit for the Dynamical Organization Of Deep Learning Loss Landscapes, or DOODL3. DOODL3 formulates the training of neural networks as a dynamical system, analyzes the learning process, and presents an interpretable global view of trajectories in the loss landscape. Our approach uses the coarseness of topology to capture the granularity of geometry to mitigate against states of instability or elongated training. Overall, our analysis presents an empirical framework to extract the global dynamics of a model and to use that information to guide the training of neural networks.