Informativeness of Weighted Conformal Prediction

Weighted conformal prediction (WCP), a recently proposed framework, provides uncertainty quantification with the flexibility to accommodate different covariate distributions between training and test data. However, it is pointed out in this paper that the effectiveness of WCP heavily relies on the overlap between covariate distributions; insufficient overlap can lead to uninformative prediction intervals. To enhance the informativeness of WCP, we propose two methods for scenarios involving multiple sources with varied covariate distributions. We establish theoretical guarantees for our proposed methods and demonstrate their efficacy through simulations.

A Unified Gaussian Process for Branching and Nested Hyperparameter Optimization

Choosing appropriate hyperparameters plays a crucial role in the success of neural networks as hyper-parameters directly control the behavior and performance of the training algorithms. To obtain efficient tuning, Bayesian optimization methods based on Gaussian process (GP) models are widely used. Despite numerous applications of Bayesian optimization in deep learning, the existing methodologies are developed based on a convenient but restrictive assumption that the tuning parameters are independent of each other. However, tuning parameters with conditional dependence are common in practice. In this paper, we focus on two types of them: branching and nested parameters. Nested parameters refer to those tuning parameters that exist only within a particular setting of another tuning parameter, and a parameter within which other parameters are nested is called a branching parameter. To capture the conditional dependence between branching and nested parameters, a unified Bayesian optimization framework is proposed. The sufficient conditions are rigorously derived to guarantee the validity of the kernel function, and the asymptotic convergence of the proposed optimization framework is proven under the continuum-armed-bandit setting. Based on the new GP model, which accounts for the dependent structure among input variables through a new kernel function, higher prediction accuracy and better optimization efficiency are observed in a series of synthetic simulations and real data applications of neural networks. Sensitivity analysis is also performed to provide insights into how changes in hyperparameter values affect prediction accuracy.

Data-Efficient Characterization of the Global Dynamics of Robot Controllers with Confidence Guarantees

This paper proposes an integration of surrogate modeling and topology to significantly reduce the amount of data required to describe the underlying global dynamics of robot controllers, including closed-box ones. A Gaussian Process (GP), trained with randomized short trajectories over the state-space, acts as a surrogate model for the underlying dynamical system. Then, a combinatorial representation is built and used to describe the dynamics in the form of a directed acyclic graph, known as {\it Morse graph}. The Morse graph is able to describe the system's attractors and their corresponding regions of attraction (\roa). Furthermore, a pointwise confidence level of the global dynamics estimation over the entire state space is provided. In contrast to alternatives, the framework does not require estimation of Lyapunov functions, alleviating the need for high prediction accuracy of the GP. The framework is suitable for data-driven controllers that do not expose an analytical model as long as Lipschitz-continuity is satisfied. The method is compared against established analytical and recent machine learning alternatives for estimating \roa s, outperforming them in data efficiency without sacrificing accuracy. Link to code: https://go.rutgers.edu/49hy35en

CLAIMED: A CLAssification-Incorporated Minimum Energy Design to explore a multivariate response surface with feasibility constraints

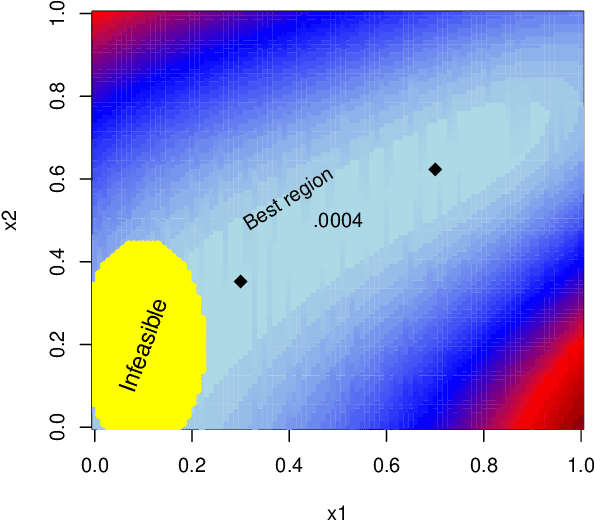
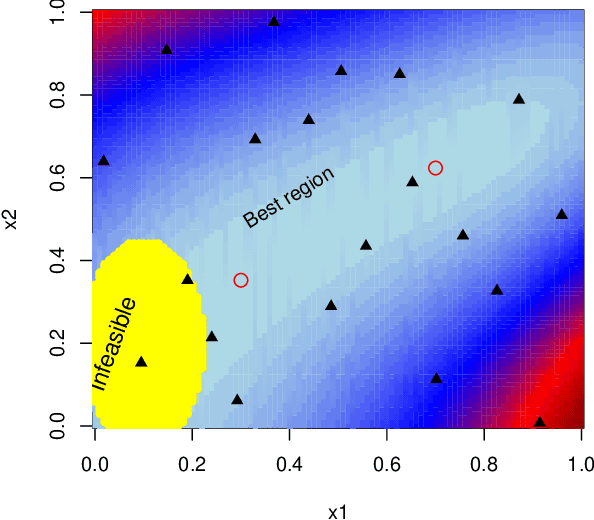
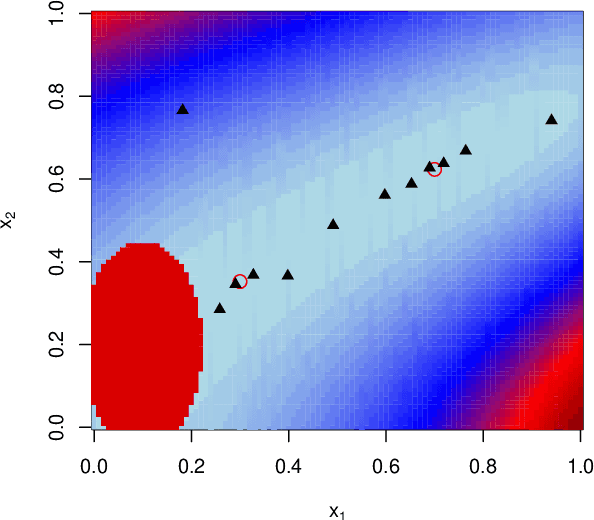
Motivated by the problem of optimization of force-field systems in physics using large-scale computer simulations, we consider exploration of a deterministic complex multivariate response surface. The objective is to find input combinations that generate output close to some desired or "target" vector. In spite of reducing the problem to exploration of the input space with respect to a one-dimensional loss function, the search is nontrivial and challenging due to infeasible input combinations, high dimensionalities of the input and output space and multiple "desirable" regions in the input space and the difficulty of emulating the objective function well with a surrogate model. We propose an approach that is based on combining machine learning techniques with smart experimental design ideas to locate multiple good regions in the input space.