Selective Conformal Risk Control

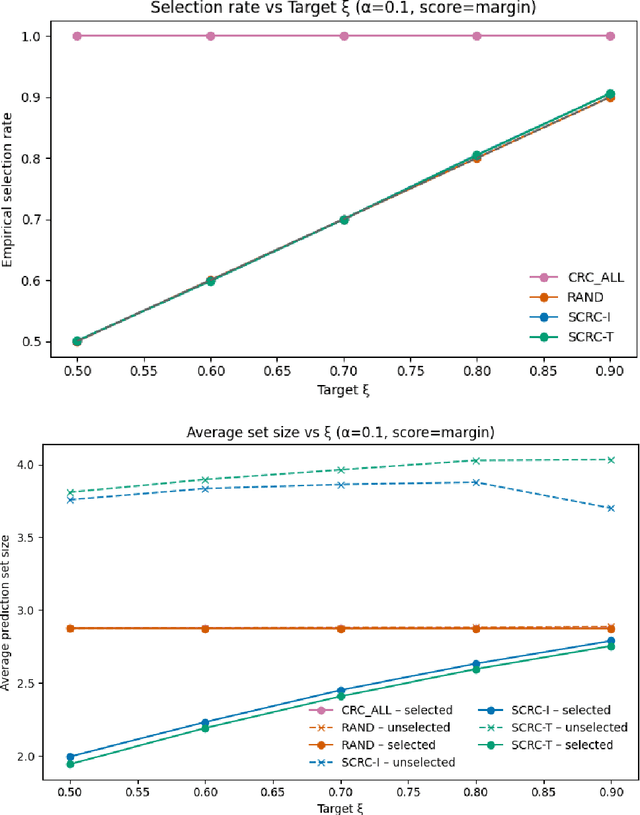
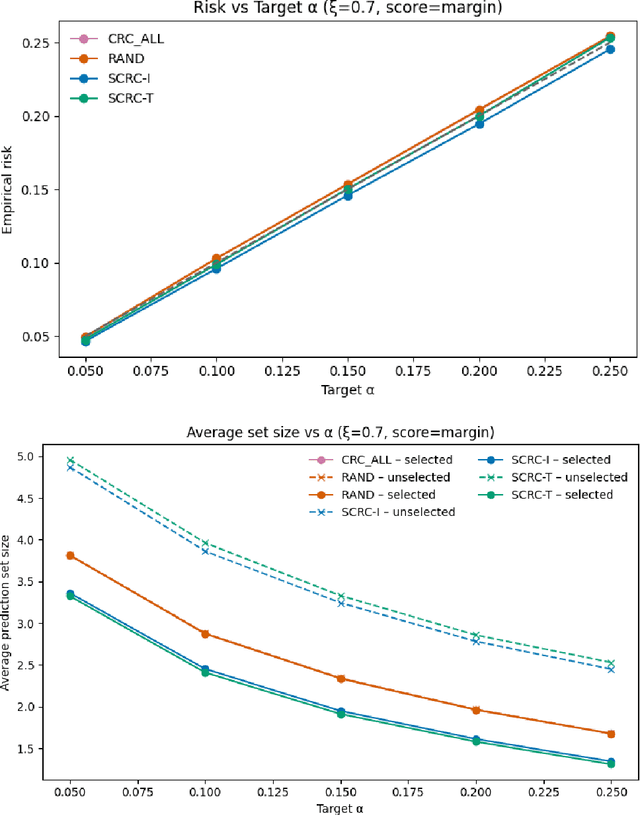
Reliable uncertainty quantification is essential for deploying machine learning systems in high-stakes domains. Conformal prediction provides distribution-free coverage guarantees but often produces overly large prediction sets, limiting its practical utility. To address this issue, we propose \textit{Selective Conformal Risk Control} (SCRC), a unified framework that integrates conformal prediction with selective classification. The framework formulates uncertainty control as a two-stage problem: the first stage selects confident samples for prediction, and the second stage applies conformal risk control on the selected subset to construct calibrated prediction sets. We develop two algorithms under this framework. The first, SCRC-T, preserves exchangeability by computing thresholds jointly over calibration and test samples, offering exact finite-sample guarantees. The second, SCRC-I, is a calibration-only variant that provides PAC-style probabilistic guarantees while being more computational efficient. Experiments on two public datasets show that both methods achieve the target coverage and risk levels, with nearly identical performance, while SCRC-I exhibits slightly more conservative risk control but superior computational practicality. Our results demonstrate that selective conformal risk control offers an effective and efficient path toward compact, reliable uncertainty quantification.

Informativeness of Weighted Conformal Prediction

Weighted conformal prediction (WCP), a recently proposed framework, provides uncertainty quantification with the flexibility to accommodate different covariate distributions between training and test data. However, it is pointed out in this paper that the effectiveness of WCP heavily relies on the overlap between covariate distributions; insufficient overlap can lead to uninformative prediction intervals. To enhance the informativeness of WCP, we propose two methods for scenarios involving multiple sources with varied covariate distributions. We establish theoretical guarantees for our proposed methods and demonstrate their efficacy through simulations.

Conformal Risk Control for Ordinal Classification

As a natural extension to the standard conformal prediction method, several conformal risk control methods have been recently developed and applied to various learning problems. In this work, we seek to control the conformal risk in expectation for ordinal classification tasks, which have broad applications to many real problems. For this purpose, we firstly formulated the ordinal classification task in the conformal risk control framework, and provided theoretic risk bounds of the risk control method. Then we proposed two types of loss functions specially designed for ordinal classification tasks, and developed corresponding algorithms to determine the prediction set for each case to control their risks at a desired level. We demonstrated the effectiveness of our proposed methods, and analyzed the difference between the two types of risks on three different datasets, including a simulated dataset, the UTKFace dataset and the diabetic retinopathy detection dataset.

Conformal Ranked Retrieval

Given the wide adoption of ranked retrieval techniques in various information systems that significantly impact our daily lives, there is an increasing need to assess and address the uncertainty inherent in their predictions. This paper introduces a novel method using the conformal risk control framework to quantitatively measure and manage risks in the context of ranked retrieval problems. Our research focuses on a typical two-stage ranked retrieval problem, where the retrieval stage generates candidates for subsequent ranking. By carefully formulating the conformal risk for each stage, we have developed algorithms to effectively control these risks within their specified bounds. The efficacy of our proposed methods has been demonstrated through comprehensive experiments on three large-scale public datasets for ranked retrieval tasks, including the MSLR-WEB dataset, the Yahoo LTRC dataset and the MS MARCO dataset.

Conformalized Ordinal Classification with Marginal and Conditional Coverage

Conformal prediction is a general distribution-free approach for constructing prediction sets combined with any machine learning algorithm that achieve valid marginal or conditional coverage in finite samples. Ordinal classification is common in real applications where the target variable has natural ordering among the class labels. In this paper, we discuss constructing distribution-free prediction sets for such ordinal classification problems by leveraging the ideas of conformal prediction and multiple testing with FWER control. Newer conformal prediction methods are developed for constructing contiguous and non-contiguous prediction sets based on marginal and conditional (class-specific) conformal $p$-values, respectively. Theoretically, we prove that the proposed methods respectively achieve satisfactory levels of marginal and class-specific conditional coverages. Through simulation study and real data analysis, these proposed methods show promising performance compared to the existing conformal method.