On the Capacity of Correlated MIMO Phase-Noise Channels: An Electro-Optic Frequency Comb Example

The capacity of a discrete-time multiple-input-multiple-output channel with correlated phase noises is investigated. In particular, the electro-optic frequency comb system is considered, where the phase noise of each channel is a combination of two independent Wiener phase-noise sources. Capacity upper and lower bounds are derived for this channel and are compared with lower bounds obtained by numerically evaluating the achievable information rates using quadrature amplitude modulation constellations. Capacity upper and lower bounds are provided for the high signal-to-noise ratio (SNR) regime. The multiplexing gain (pre-log) is shown to be $M-1$, where $M$ represents the number of channels. A constant gap between the asymptotic upper and lower bounds is observed, which depends on the number of channels $M$. For the specific case of $M=2$, capacity is characterized up to a term that vanishes as the SNR grows large.

Pilot Distributions for Phase Noise Estimation in Electro-Optic Frequency Comb Systems

We explore the optimal pilot positioning for phase tracking in electro-optic frequency comb setups. We show that, in contrast to previous results for regular multichannel systems, allocating the first and the last channels for pilots is optimal given a fixed pilot overhead

Learning to Extract Distributed Polarization Sensing Data from Noisy Jones Matrices

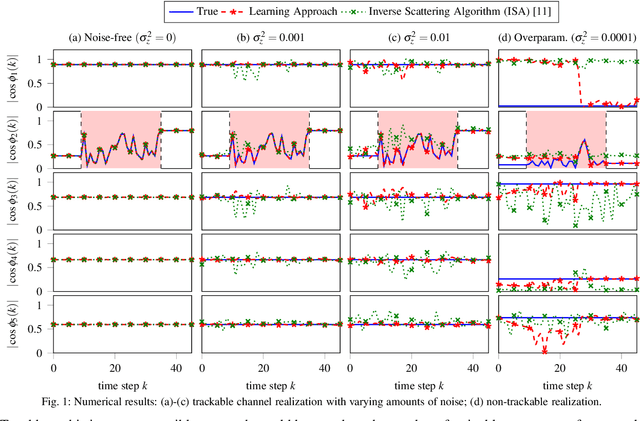
We consider the problem of recovering spatially resolved polarization information from receiver Jones matrices. We introduce a physics-based learning approach, improving noise resilience compared to previous inverse scattering methods, while highlighting challenges related to model overparameterization.

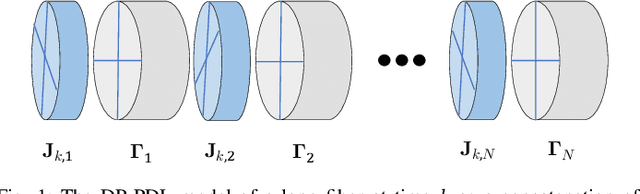
Polarization Tracking in the Presence of PDL and Fast Temporal Drift

In this paper, we analyze the effectiveness of polarization tracking algorithms in optical transmission systems suffering from fast state of polarization (SOP) rotations and polarization-dependent loss (PDL). While most of the gradient descent (GD)-based algorithms in the literature may require step size adjustment when the channel condition changes, we propose tracking algorithms that can perform similarly or better without parameter tuning. Numerical simulation results show higher robustness of the proposed algorithms to SOP and PDL drift compared to GD-based algorithms, making them promising candidates to be used in aerial fiber links where the SOP can potentially drift rapidly, and therefore becomes challenging to track.

Data-Driven Upper Bounds on Channel Capacity

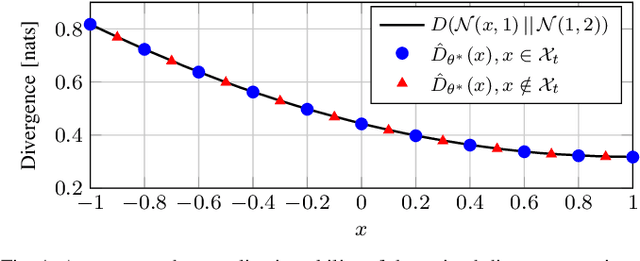
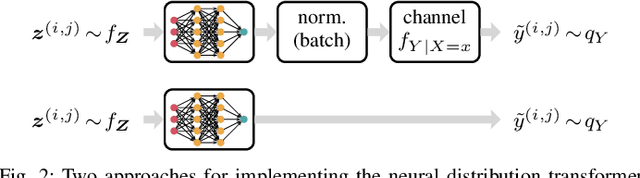
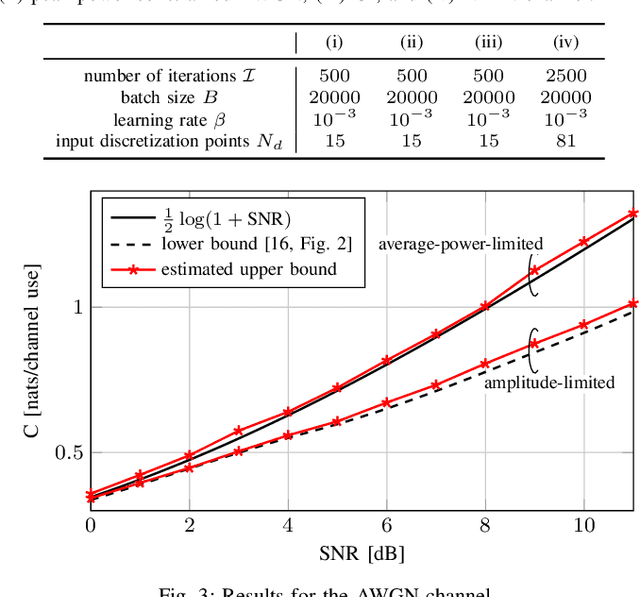
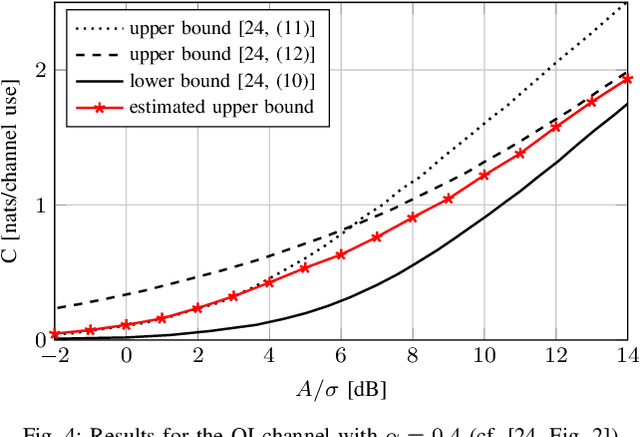
We consider the problem of estimating an upper bound on the capacity of a memoryless channel with unknown channel law and continuous output alphabet. A novel data-driven algorithm is proposed that exploits the dual representation of capacity where the maximization over the input distribution is replaced with a minimization over a reference distribution on the channel output. To efficiently compute the required divergence maximization between the conditional channel and the reference distribution, we use a modified mutual information neural estimator that takes the channel input as an additional parameter. We evaluate our approach on different memoryless channels and show that the estimated upper bounds closely converge either to the channel capacity or to best-known lower bounds.

Benchmarking and Interpreting End-to-end Learning of MIMO and Multi-User Communication

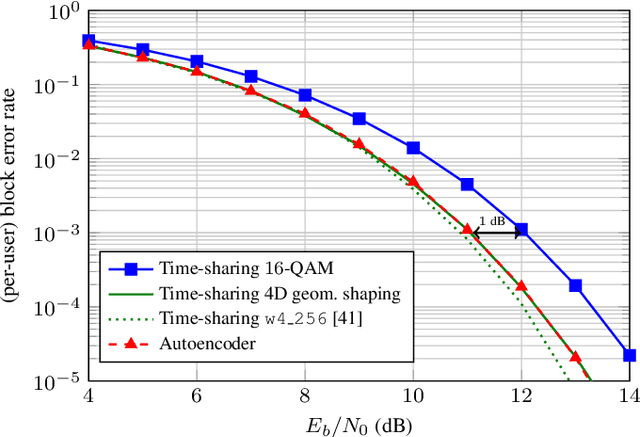
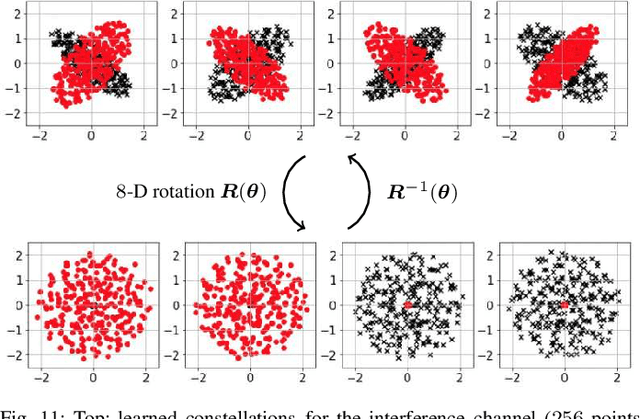
End-to-end autoencoder (AE) learning has the potential of exceeding the performance of human-engineered transceivers and encoding schemes, without a priori knowledge of communication-theoretic principles. In this work, we aim to understand to what extent and for which scenarios this claim holds true when comparing with fair benchmarks. Our particular focus is on memoryless multiple-input multiple-output (MIMO) and multi-user (MU) systems. Four case studies are considered: two point-to-point (closed-loop and open-loop MIMO) and two MU scenarios (MIMO broadcast and interference channels). For the point-to-point scenarios, we explain some of the performance gains observed in prior work through the selection of improved baseline schemes that include geometric shaping as well as bit and power allocation. For the MIMO broadcast channel, we demonstrate the feasibility of a novel AE method with centralized learning and decentralized execution. Interestingly, the learned scheme performs close to nonlinear vector-perturbation precoding and significantly outperforms conventional zero-forcing. Lastly, we highlight potential pitfalls when interpreting learned communication schemes. In particular, we show that the AE for the considered interference channel learns to avoid interference, albeit in a rotated reference frame. After de-rotating the learned signal constellation of each user, the resulting scheme corresponds to conventional time sharing with geometric shaping.

Capacity Bounds under Imperfect Polarization Tracking

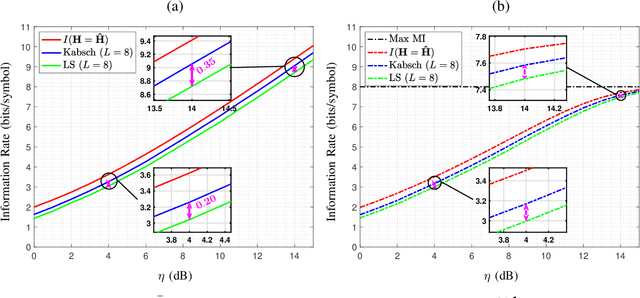
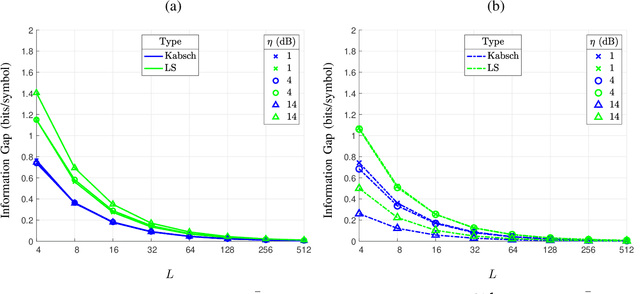
In optical fiber communication, due to the random variation of the environment, the state of polarization (SOP) fluctuates randomly with time leading to distortion and performance degradation. The memory-less SOP fluctuations can be regarded as a two-by-two random unitary matrix. In this paper, for what we believe to be the first time, the capacity of the polarization drift channel under an average power constraint with imperfect channel knowledge is characterized. An achievable information rate (AIR) is derived when imperfect channel knowledge is available and is shown to be highly dependent on the channel estimation technique. It is also shown that a tighter lower bound can be achieved when a unitary estimation of the channel is available. However, the conventional estimation algorithms do not guarantee a unitary channel estimation. Therefore, by considering the unitary constraint of the channel, a data-aided channel estimator based on the Kabsch algorithm is proposed, and its performance is numerically evaluated in terms of AIR. Monte Carlo simulations show that Kabsch outperforms the least-square error algorithm. In particular, with complex, Gaussian inputs and eight pilot symbols per block, Kabsch improves the AIR by 0:2 to 0:35 bits/symbol throughout the range of studied signal-to-noise ratios.

Frequency Logarithmic Perturbation on the Group-Velocity Dispersion Parameter with Applications to Passive Optical Networks

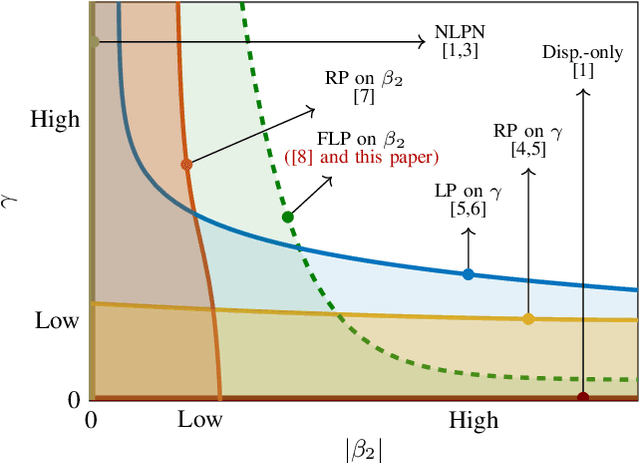
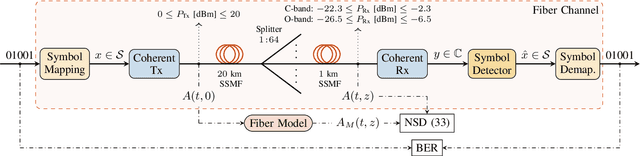
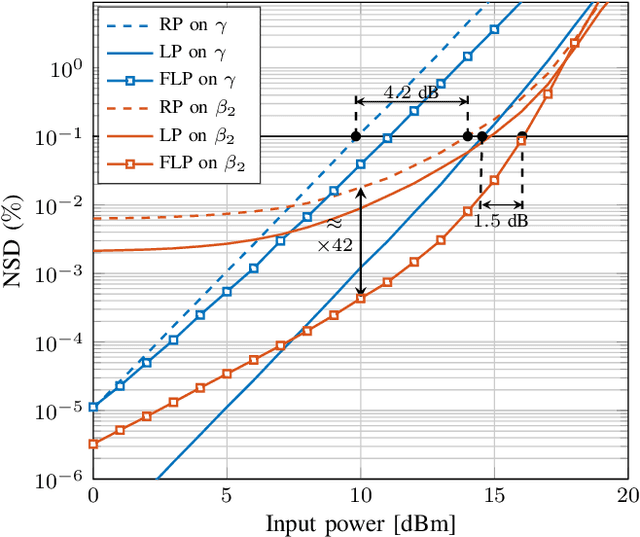
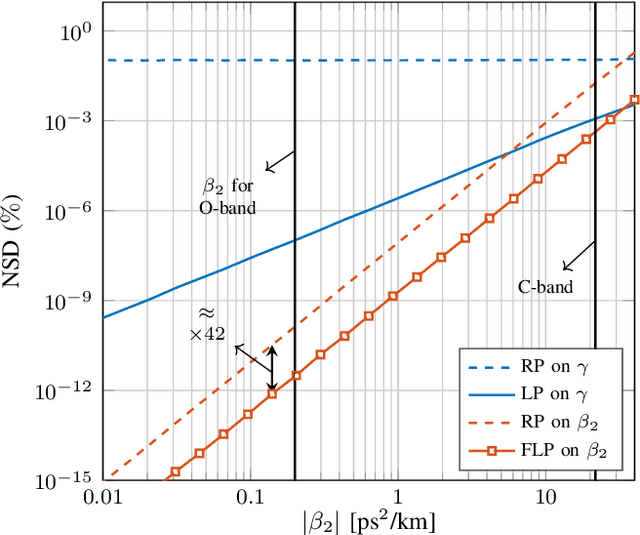
Signal propagation in an optical fiber can be described by the nonlinear Schr\"odinger equation (NLSE). The NLSE has no known closed-form solution, mostly due to the interaction of dispersion and nonlinearities. In this paper, we present a novel closed-form approximate model for the nonlinear optical channel, with applications to passive optical networks. The proposed model is derived using logarithmic perturbation in the frequency domain on the group-velocity dispersion (GVD) parameter of the NLSE. The model can be seen as an improvement of the recently proposed regular perturbation (RP) on the GVD parameter. RP and logarithmic perturbation (LP) on the nonlinear coefficient have already been studied in the literature, and are hereby compared with RP on the GVD parameter and the proposed LP model. As an application of the model, we focus on passive optical networks. For a 20 km PON at 10 Gbaud, the proposed model improves upon LP on the nonlinear coefficient by 1.5 dB. For the same system, a detector based on the proposed LP model reduces the uncoded bit-error-rate by up to 5.4 times at the same input power or reduces the input power by 0.4 dB at the same information rate.

Compressed Shaping: Concept and FPGA Demonstration

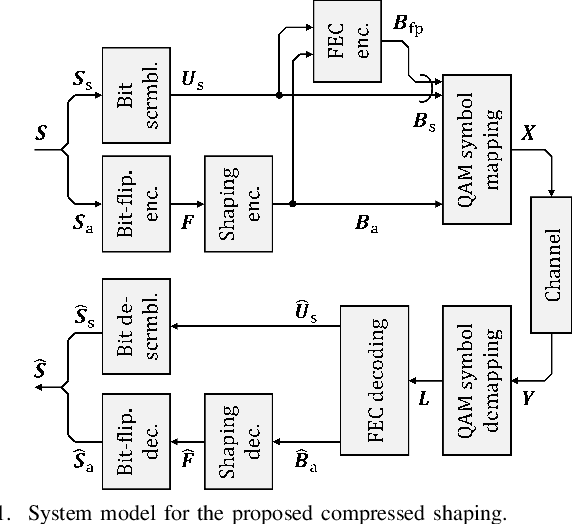
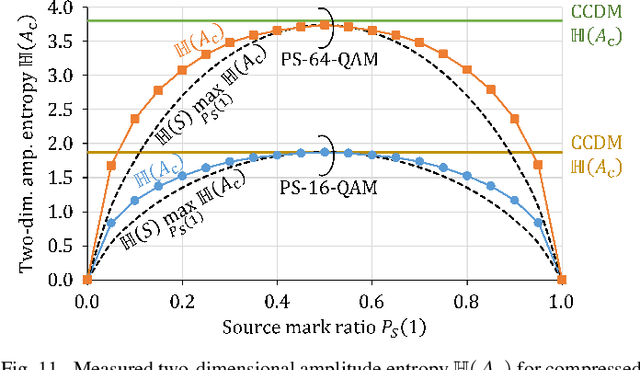
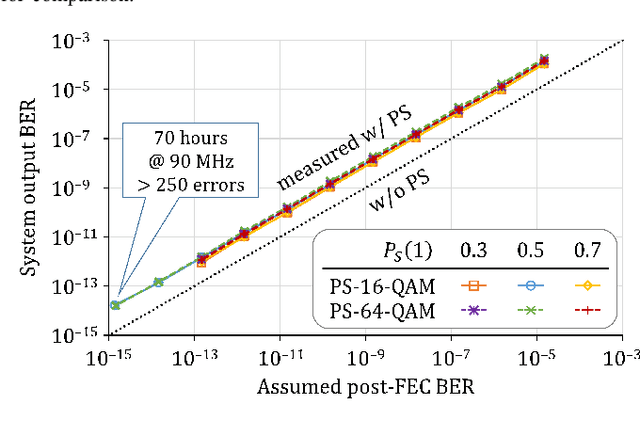
Probabilistic shaping (PS) has been widely studied and applied to optical fiber communications. The encoder of PS expends the number of bit slots and controls the probability distribution of channel input symbols. Not only studies focused on PS but also most works on optical fiber communications have assumed source uniformity (i.e. equal probability of marks and spaces) so far. On the other hand, the source information is in general nonuniform, unless bit-scrambling or other source coding techniques to balance the bit probability is performed. Interestingly,one can exploit the source nonuniformity to reduce the entropy of the channel input symbols with the PS encoder, which leads to smaller required signal-to-noise ratio at a given input logic rate. This benefit is equivalent to a combination of data compression and PS, and thus we call this technique compressed shaping. In this work, we explain its theoretical background in detail, and verify the concept by both numerical simulation and a field programmable gate array (FPGA) implementation of such a system. In particular, we find that compressed shaping can reduce power consumption in forward error correction decoding by up to 90% in nonuniform source cases. The additional hardware resources required for compressed shaping are not significant compared with forward error correction coding, and a real-time back-to-back test is successfully demonstrated.

End-to-End Learning of Geometrical Shaping Maximizing Generalized Mutual Information

GMI-based end-to-end learning is shown to be highly nonconvex. We apply gradient descent initialized with Gray-labeled APSK constellations directly to the constellation coordinates. State-of-the-art constellations in 2D and 4D are found providing reach increases up to 26\% w.r.t. to QAM.