Capacity Bounds under Imperfect Polarization Tracking

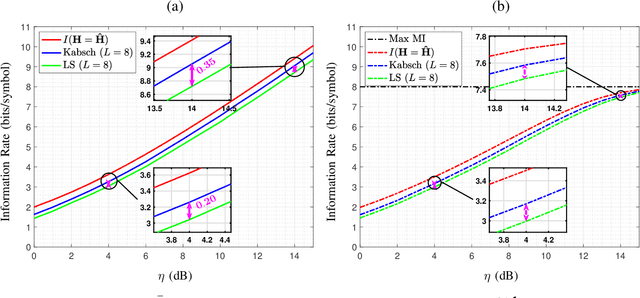
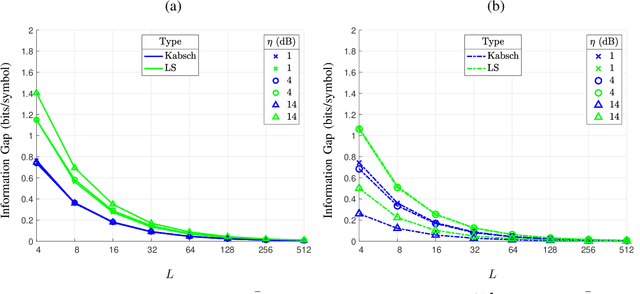
In optical fiber communication, due to the random variation of the environment, the state of polarization (SOP) fluctuates randomly with time leading to distortion and performance degradation. The memory-less SOP fluctuations can be regarded as a two-by-two random unitary matrix. In this paper, for what we believe to be the first time, the capacity of the polarization drift channel under an average power constraint with imperfect channel knowledge is characterized. An achievable information rate (AIR) is derived when imperfect channel knowledge is available and is shown to be highly dependent on the channel estimation technique. It is also shown that a tighter lower bound can be achieved when a unitary estimation of the channel is available. However, the conventional estimation algorithms do not guarantee a unitary channel estimation. Therefore, by considering the unitary constraint of the channel, a data-aided channel estimator based on the Kabsch algorithm is proposed, and its performance is numerically evaluated in terms of AIR. Monte Carlo simulations show that Kabsch outperforms the least-square error algorithm. In particular, with complex, Gaussian inputs and eight pilot symbols per block, Kabsch improves the AIR by 0:2 to 0:35 bits/symbol throughout the range of studied signal-to-noise ratios.