High-Cardinality Hybrid Shaping for 4D Modulation Formats in Optical Communications Optimized via End-to-End Learning

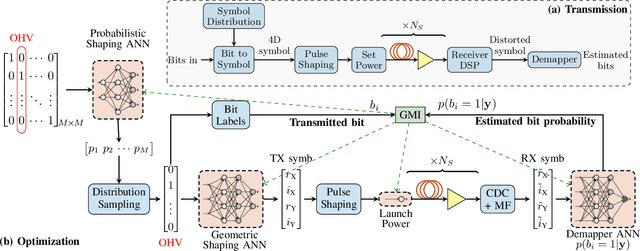
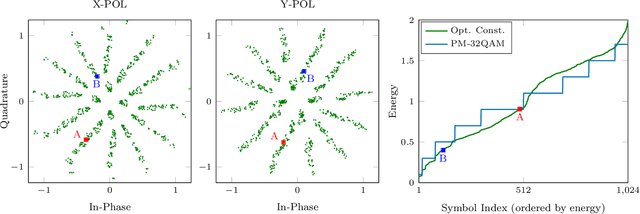
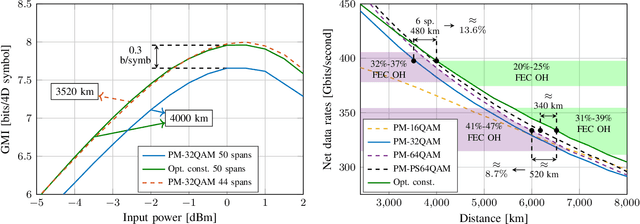
In this paper we carry out a joint optimization of probabilistic (PS) and geometric shaping (GS) for four-dimensional (4D) modulation formats in long-haul coherent wavelength division multiplexed (WDM) optical fiber communications using an auto-encoder framework. We propose a 4D 10 bits/symbol constellation which we obtained via end-to-end deep learning over the split-step Fourier model of the fiber channel. The constellation achieved 13.6% reach increase at a data rate of approximately 400 Gbits/second in comparison to the ubiquitously employed polarization multiplexed 32-QAM format at a forward error correction overhead of 20%.

Frequency Logarithmic Perturbation on the Group-Velocity Dispersion Parameter with Applications to Passive Optical Networks

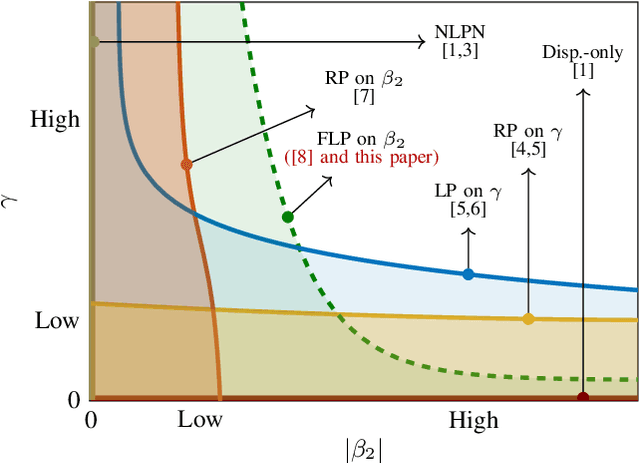
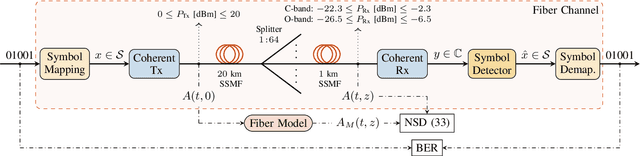
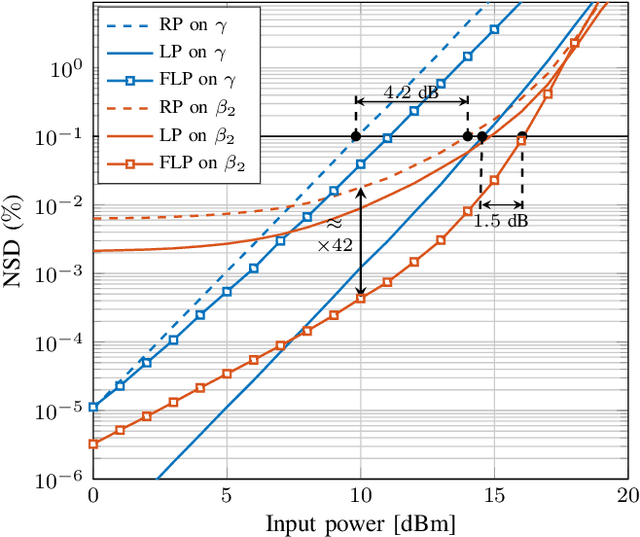
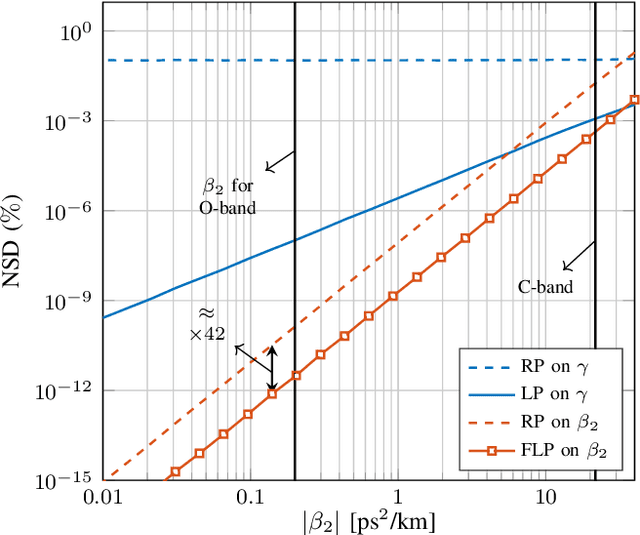
Signal propagation in an optical fiber can be described by the nonlinear Schr\"odinger equation (NLSE). The NLSE has no known closed-form solution, mostly due to the interaction of dispersion and nonlinearities. In this paper, we present a novel closed-form approximate model for the nonlinear optical channel, with applications to passive optical networks. The proposed model is derived using logarithmic perturbation in the frequency domain on the group-velocity dispersion (GVD) parameter of the NLSE. The model can be seen as an improvement of the recently proposed regular perturbation (RP) on the GVD parameter. RP and logarithmic perturbation (LP) on the nonlinear coefficient have already been studied in the literature, and are hereby compared with RP on the GVD parameter and the proposed LP model. As an application of the model, we focus on passive optical networks. For a 20 km PON at 10 Gbaud, the proposed model improves upon LP on the nonlinear coefficient by 1.5 dB. For the same system, a detector based on the proposed LP model reduces the uncoded bit-error-rate by up to 5.4 times at the same input power or reduces the input power by 0.4 dB at the same information rate.