Data-Driven Upper Bounds on Channel Capacity

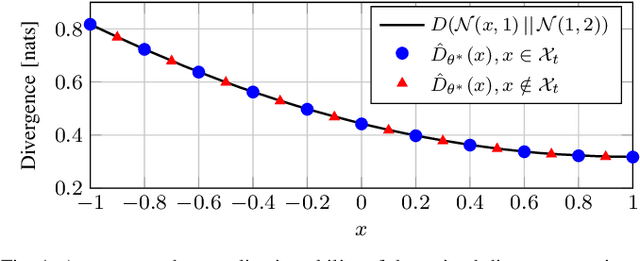
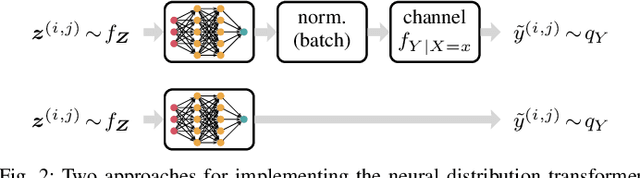
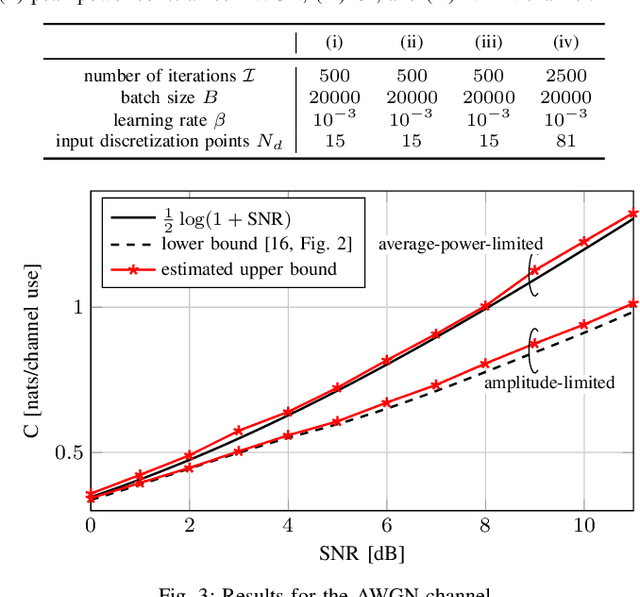
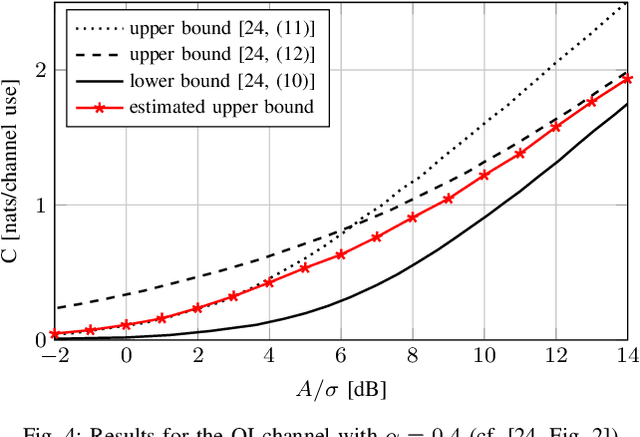
We consider the problem of estimating an upper bound on the capacity of a memoryless channel with unknown channel law and continuous output alphabet. A novel data-driven algorithm is proposed that exploits the dual representation of capacity where the maximization over the input distribution is replaced with a minimization over a reference distribution on the channel output. To efficiently compute the required divergence maximization between the conditional channel and the reference distribution, we use a modified mutual information neural estimator that takes the channel input as an additional parameter. We evaluate our approach on different memoryless channels and show that the estimated upper bounds closely converge either to the channel capacity or to best-known lower bounds.