Continuous Monitoring via Repeated Significance

Requiring statistical significance at multiple interim analyses to declare a statistically significant result for an AB test allows less stringent requirements for significance at each interim analysis. Repeated repeated significance competes well with methods built on assumptions about the test -- assumptions that may be impossible to evaluate a priori and may require extra data to evaluate empirically. Instead, requiring repeated significance allows the data itself to prove directly that the required results are not due to chance alone. We explain how to apply tests with repeated significance to continuously monitor unbounded tests -- tests that do not have an a priori bound on running time or number of observations. We show that it is impossible to maintain a constant requirement for significance for unbounded tests, but that we can come arbitrarily close to that goal.

Early Stopping Based on Repeated Significance

For a bucket test with a single criterion for success and a fixed number of samples or testing period, requiring a $p$-value less than a specified value of $\alpha$ for the success criterion produces statistical confidence at level $1 - \alpha$. For multiple criteria, a Bonferroni correction that partitions $\alpha$ among the criteria produces statistical confidence, at the cost of requiring lower $p$-values for each criterion. The same concept can be applied to decisions about early stopping, but that can lead to strict requirements for $p$-values. We show how to address that challenge by requiring criteria to be successful at multiple decision points.

Non-asymptotic approximations for Pearson's chi-square statistic and its application to confidence intervals for strictly convex functions of the probability weights of discrete distributions

In this paper, we develop a non-asymptotic local normal approximation for multinomial probabilities. First, we use it to find non-asymptotic total variation bounds between the measures induced by uniformly jittered multinomials and the multivariate normals with the same means and covariances. From the total variation bounds, we also derive a comparison of the cumulative distribution functions and quantile coupling inequalities between Pearson's chi-square statistic (written as the normalized quadratic form of a multinomial vector) and its multivariate normal analogue. We apply our results to find confidence intervals for the negative entropy of discrete distributions. Our method can be applied more generally to find confidence intervals for strictly convex functions of the weights of discrete distributions.

Sharp Frequency Bounds for Sample-Based Queries

A data sketch algorithm scans a big data set, collecting a small amount of data -- the sketch, which can be used to statistically infer properties of the big data set. Some data sketch algorithms take a fixed-size random sample of a big data set, and use that sample to infer frequencies of items that meet various criteria in the big data set. This paper shows how to statistically infer probably approximately correct (PAC) bounds for those frequencies, efficiently, and precisely enough that the frequency bounds are either sharp or off by only one, which is the best possible result without exact computation.

Selecting a number of voters for a voting ensemble

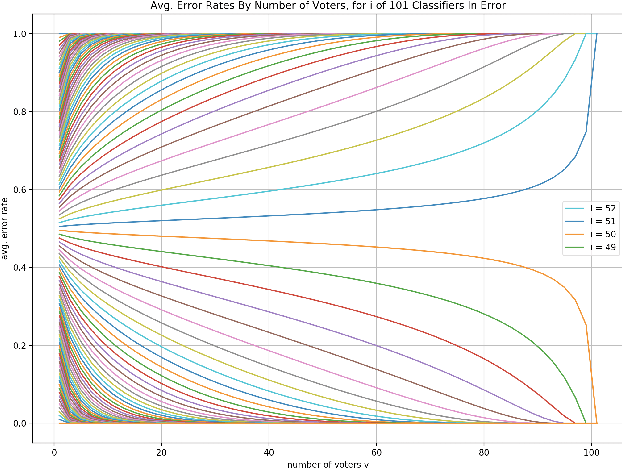
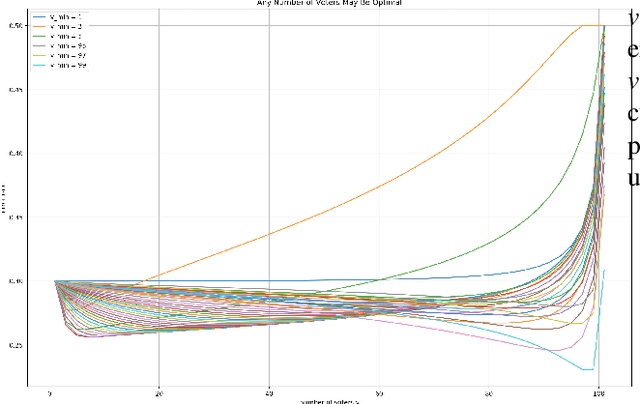
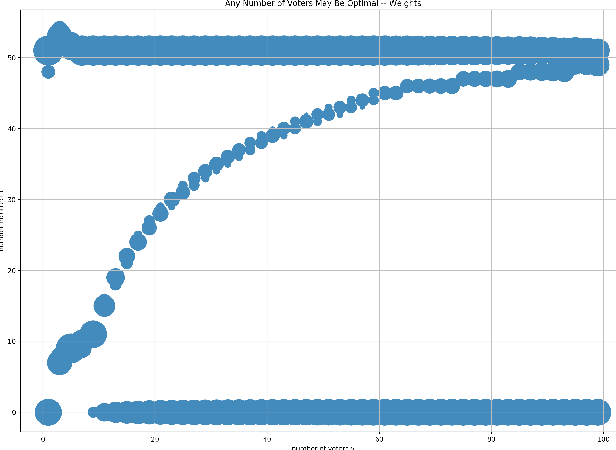
For a voting ensemble that selects an odd-sized subset of the ensemble classifiers at random for each example, applies them to the example, and returns the majority vote, we show that any number of voters may minimize the error rate over an out-of-sample distribution. The optimal number of voters depends on the out-of-sample distribution of the number of classifiers in error. To select a number of voters to use, estimating that distribution then inferring error rates for numbers of voters gives lower-variance estimates than directly estimating those error rates.

Ensemble Validation: Selectivity has a Price, but Variety is Free

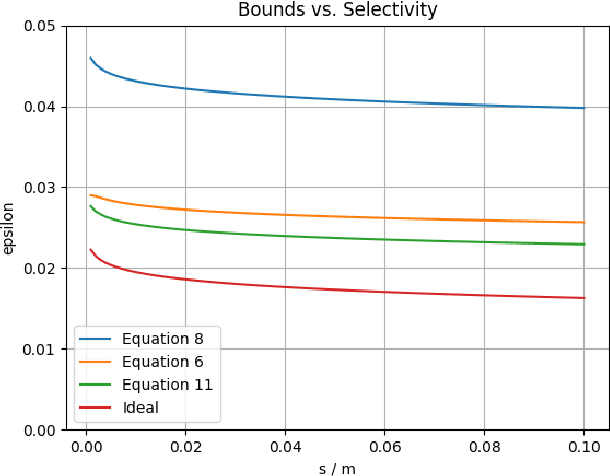
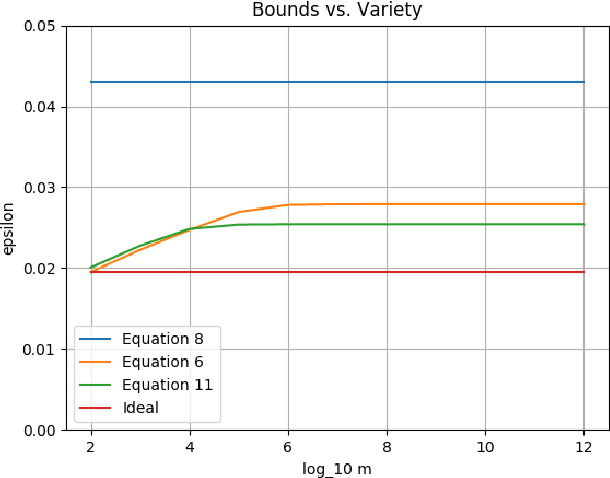
Suppose some classifiers are selected from a set of hypothesis classifiers to form an equally-weighted ensemble that selects a member classifier at random for each input example. Then the ensemble has an error bound consisting of the average error bound for the member classifiers, a term for selectivity that varies from zero (if all hypothesis classifiers are selected) to a standard uniform error bound (if only a single classifier is selected), and small constants. There is no penalty for using a richer hypothesis set if the same fraction of the hypothesis classifiers are selected for the ensemble.

Speculate-Correct Error Bounds for k-Nearest Neighbor Classifiers

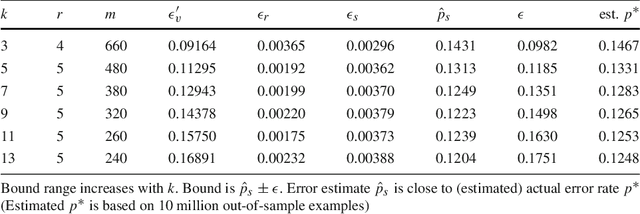
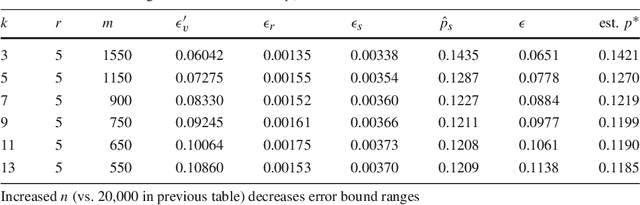
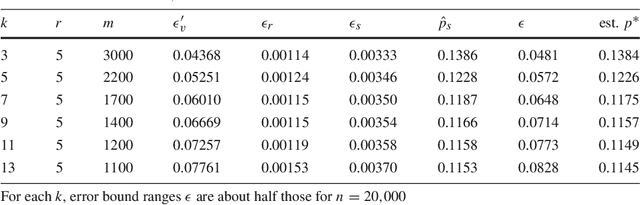
We introduce the speculate-correct method to derive error bounds for local classifiers. Using it, we show that k nearest neighbor classifiers, in spite of their famously fractured decision boundaries, have exponential error bounds with O(sqrt((k + ln n) / n)) error bound range for n in-sample examples.

Validation of Matching

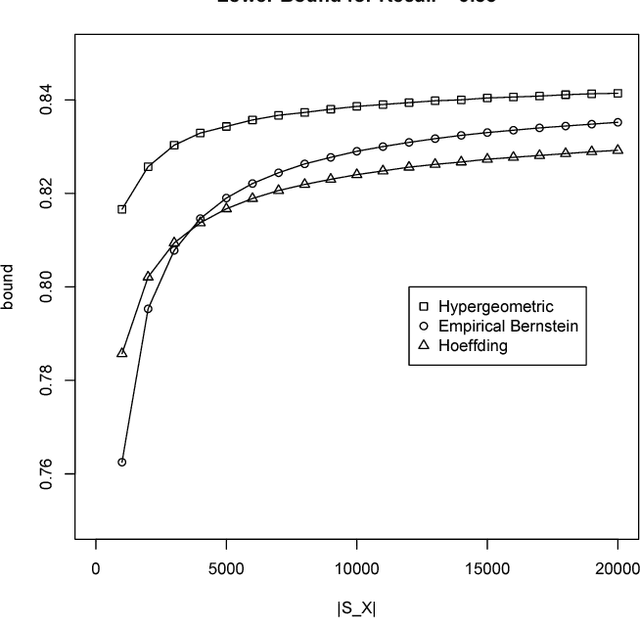
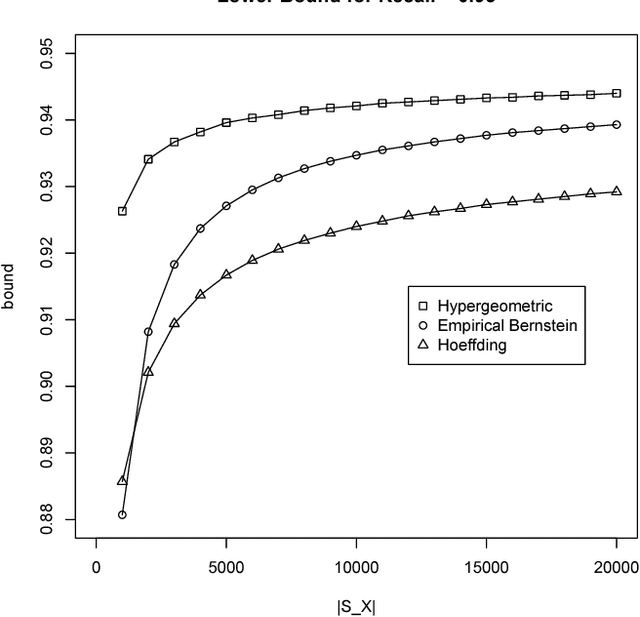
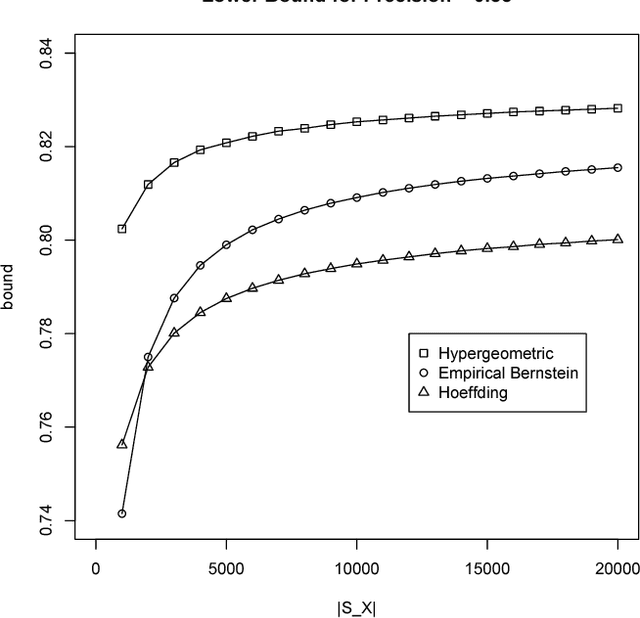
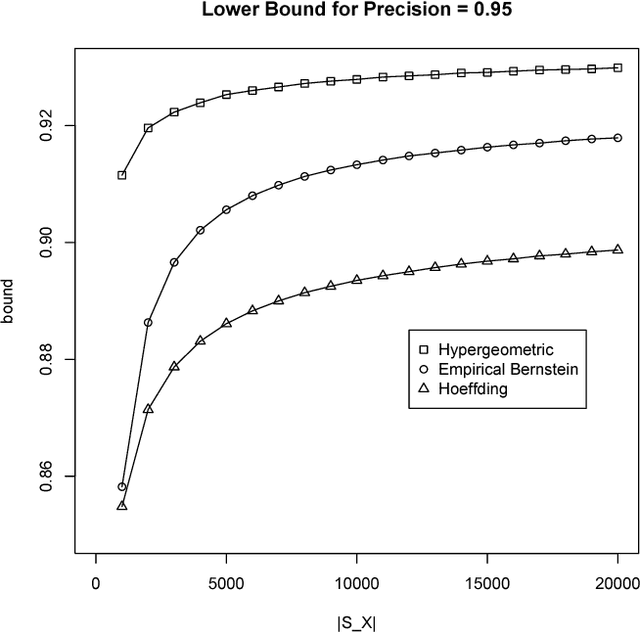
We introduce a technique to compute probably approximately correct (PAC) bounds on precision and recall for matching algorithms. The bounds require some verified matches, but those matches may be used to develop the algorithms. The bounds can be applied to network reconciliation or entity resolution algorithms, which identify nodes in different networks or values in a data set that correspond to the same entity. For network reconciliation, the bounds do not require knowledge of the network generation process.

Some Theory For Practical Classifier Validation

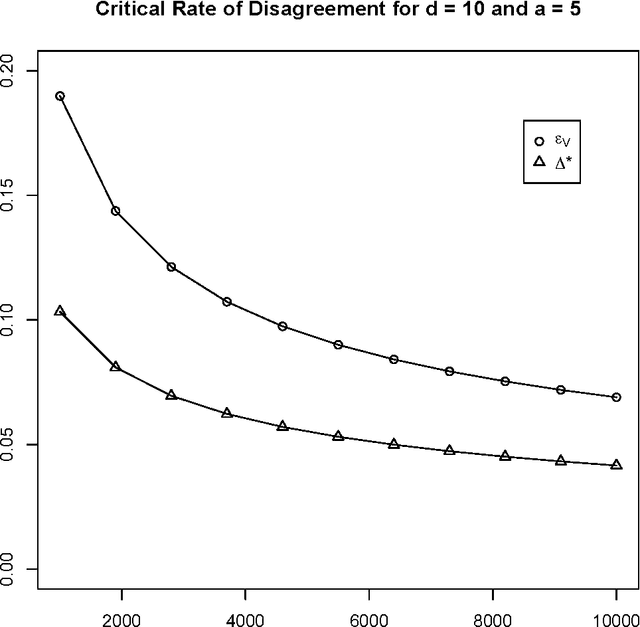
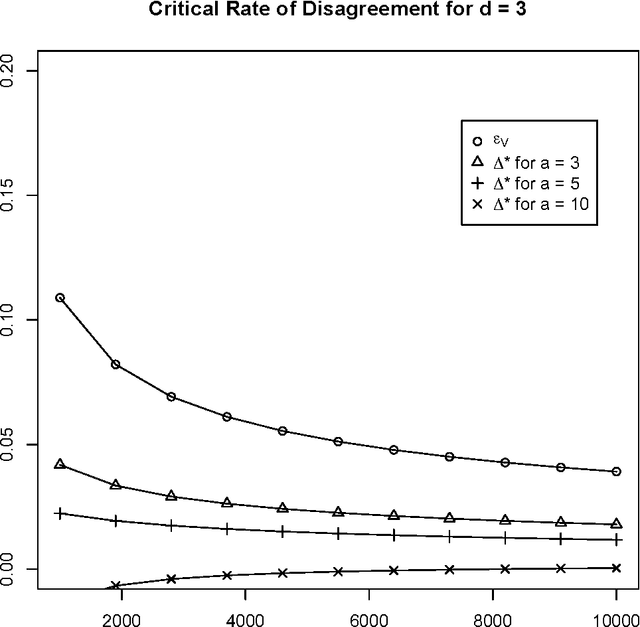
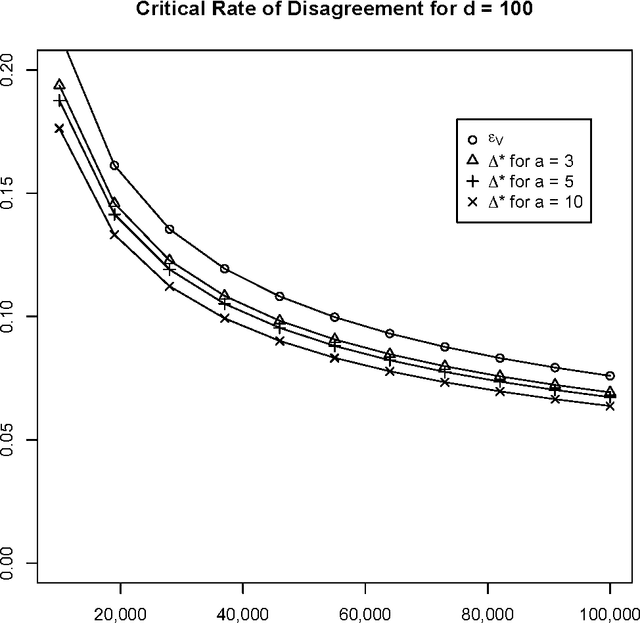
We compare and contrast two approaches to validating a trained classifier while using all in-sample data for training. One is simultaneous validation over an organized set of hypotheses (SVOOSH), the well-known method that began with VC theory. The other is withhold and gap (WAG). WAG withholds a validation set, trains a holdout classifier on the remaining data, uses the validation data to validate that classifier, then adds the rate of disagreement between the holdout classifier and one trained using all in-sample data, which is an upper bound on the difference in error rates. We show that complex hypothesis classes and limited training data can make WAG a favorable alternative.

Improved Error Bounds Based on Worst Likely Assignments

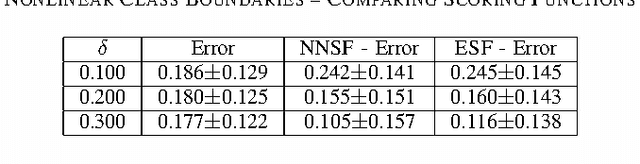
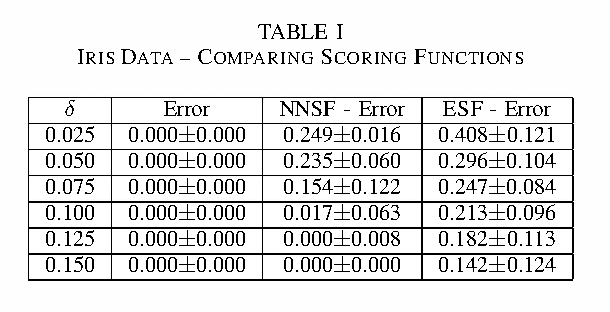
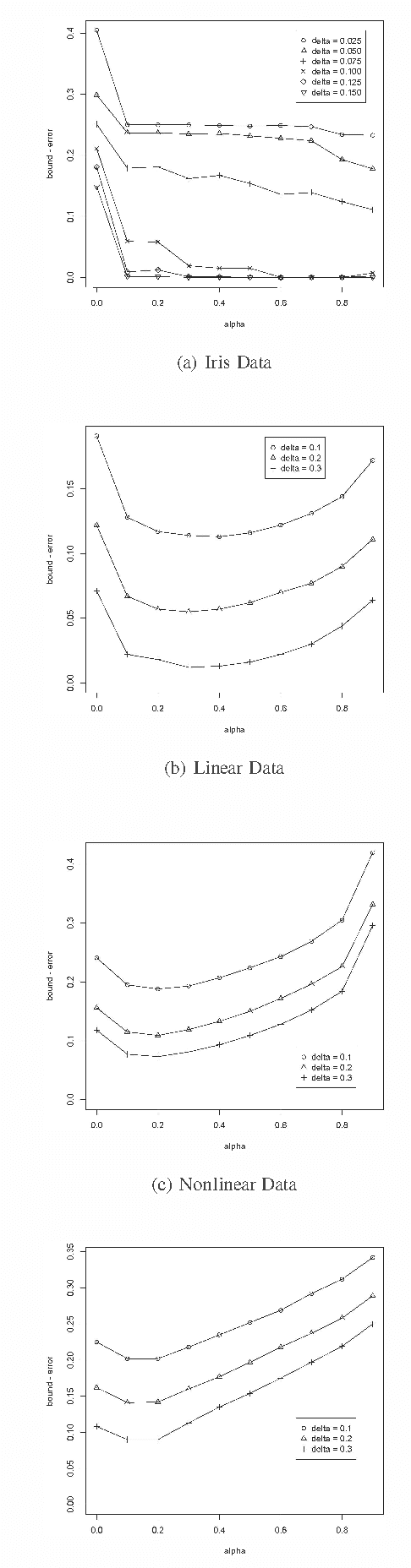
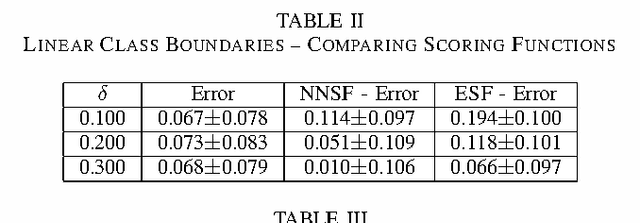
Error bounds based on worst likely assignments use permutation tests to validate classifiers. Worst likely assignments can produce effective bounds even for data sets with 100 or fewer training examples. This paper introduces a statistic for use in the permutation tests of worst likely assignments that improves error bounds, especially for accurate classifiers, which are typically the classifiers of interest.