Selecting a number of voters for a voting ensemble
Paper and Code
Apr 23, 2021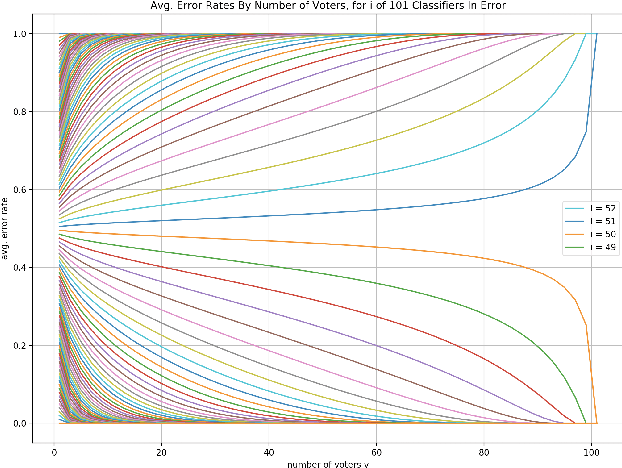
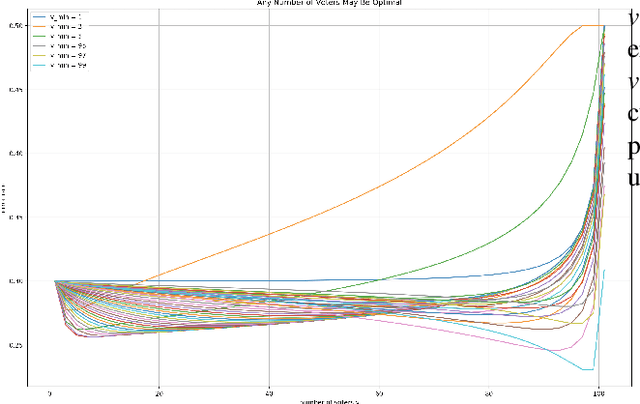
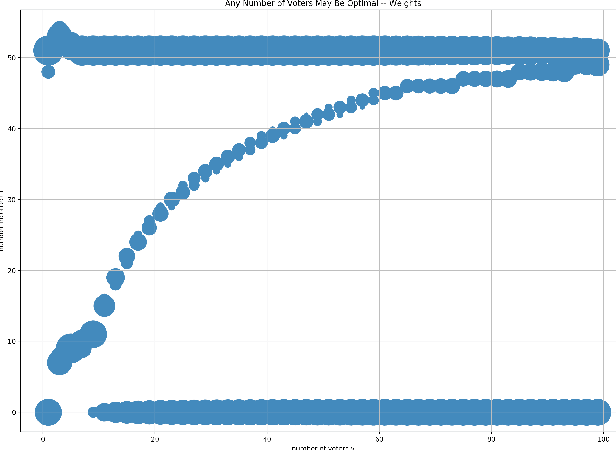
For a voting ensemble that selects an odd-sized subset of the ensemble classifiers at random for each example, applies them to the example, and returns the majority vote, we show that any number of voters may minimize the error rate over an out-of-sample distribution. The optimal number of voters depends on the out-of-sample distribution of the number of classifiers in error. To select a number of voters to use, estimating that distribution then inferring error rates for numbers of voters gives lower-variance estimates than directly estimating those error rates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge