Elija Perrier
Agent Identity Evals: Measuring Agentic Identity
Jul 23, 2025Abstract:Central to agentic capability and trustworthiness of language model agents (LMAs) is the extent they maintain stable, reliable, identity over time. However, LMAs inherit pathologies from large language models (LLMs) (statelessness, stochasticity, sensitivity to prompts and linguistically-intermediation) which can undermine their identifiability, continuity, persistence and consistency. This attrition of identity can erode their reliability, trustworthiness and utility by interfering with their agentic capabilities such as reasoning, planning and action. To address these challenges, we introduce \textit{agent identity evals} (AIE), a rigorous, statistically-driven, empirical framework for measuring the degree to which an LMA system exhibit and maintain their agentic identity over time, including their capabilities, properties and ability to recover from state perturbations. AIE comprises a set of novel metrics which can integrate with other measures of performance, capability and agentic robustness to assist in the design of optimal LMA infrastructure and scaffolding such as memory and tools. We set out formal definitions and methods that can be applied at each stage of the LMA life-cycle, and worked examples of how to apply them.
Hamiltonian Formalism for Comparing Quantum and Classical Intelligence
Jun 17, 2025Abstract:The prospect of AGI instantiated on quantum substrates motivates the development of mathematical frameworks that enable direct comparison of their operation in classical and quantum environments. To this end, we introduce a Hamiltonian formalism for describing classical and quantum AGI tasks as a means of contrasting their interaction with the environment. We propose a decomposition of AGI dynamics into Hamiltonian generators for core functions such as induction, reasoning, recursion, learning, measurement, and memory. This formalism aims to contribute to the development of a precise mathematical language for how quantum and classical agents differ via environmental interaction.
Quantum AGI: Ontological Foundations
Jun 16, 2025Abstract:We examine the implications of quantum foundations for AGI, focusing on how seminal results such as Bell's theorems (non-locality), the Kochen-Specker theorem (contextuality) and no-cloning theorem problematise practical implementation of AGI in quantum settings. We introduce a novel information-theoretic taxonomy distinguishing between classical AGI and quantum AGI and show how quantum mechanics affects fundamental features of agency. We show how quantum ontology may change AGI capabilities, both via affording computational advantages and via imposing novel constraints.
Quantum AIXI: Universal Intelligence via Quantum Information
May 27, 2025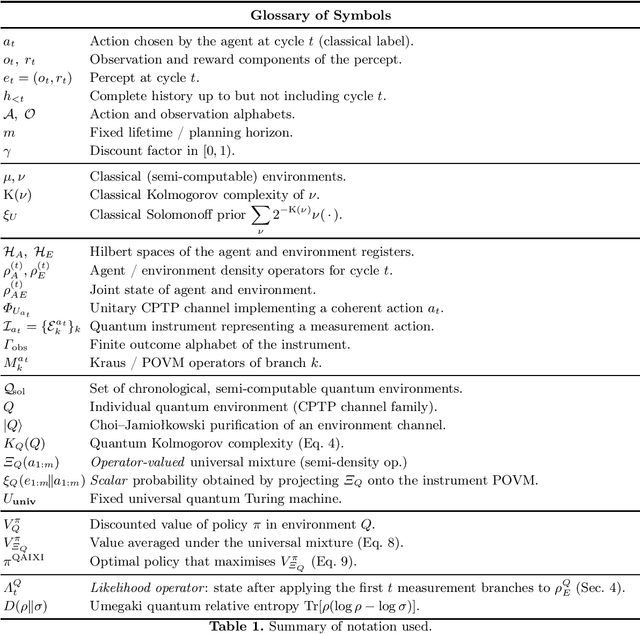
Abstract:AIXI is a widely studied model of artificial general intelligence (AGI) based upon principles of induction and reinforcement learning. However, AIXI is fundamentally classical in nature - as are the environments in which it is modelled. Given the universe is quantum mechanical in nature and the exponential overhead required to simulate quantum mechanical systems classically, the question arises as to whether there are quantum mechanical analogues of AIXI which are theoretically consistent or practically feasible as models of universal intelligence. To address this question, we extend the framework to quantum information and present Quantum AIXI (QAIXI). We introduce a model of quantum agent/environment interaction based upon quantum and classical registers and channels, showing how quantum AIXI agents may take both classical and quantum actions. We formulate the key components of AIXI in quantum information terms, extending previous research on quantum Kolmogorov complexity and a QAIXI value function. We discuss conditions and limitations upon quantum Solomonoff induction and show how contextuality fundamentally affects QAIXI models.
K-P Quantum Neural Networks
Apr 02, 2025Abstract:We present an extension of K-P time-optimal quantum control solutions using global Cartan $KAK$ decompositions for geodesic-based solutions. Extending recent time-optimal \emph{constant-$\theta$} control results, we integrate Cartan methods into equivariant quantum neural network (EQNN) for quantum control tasks. We show that a finite-depth limited EQNN ansatz equipped with Cartan layers can replicate the constant-$\theta$ sub-Riemannian geodesics for K-P problems. We demonstrate how for certain classes of control problem on Riemannian symmetric spaces, gradient-based training using an appropriate cost function converges to certain global time-optimal solutions when satisfying simple regularity conditions. This generalises prior geometric control theory methods and clarifies how optimal geodesic estimation can be performed in quantum machine learning contexts.
Statistical Scenario Modelling and Lookalike Distributions for Multi-Variate AI Risk
Feb 20, 2025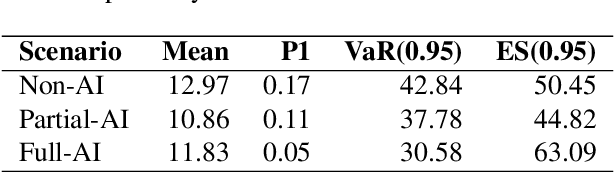
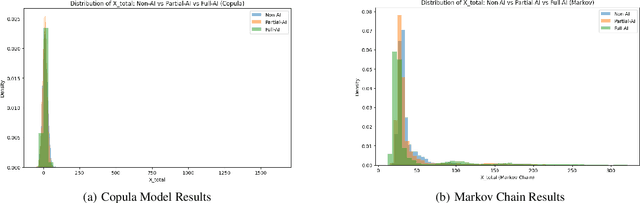
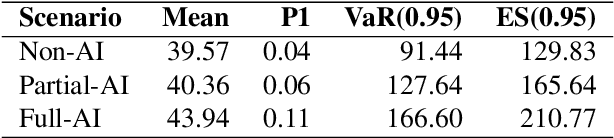
Abstract:Evaluating AI safety requires statistically rigorous methods and risk metrics for understanding how the use of AI affects aggregated risk. However, much AI safety literature focuses upon risks arising from AI models in isolation, lacking consideration of how modular use of AI affects risk distribution of workflow components or overall risk metrics. There is also a lack of statistical grounding enabling sensitisation of risk models in the presence of absence of AI to estimate causal contributions of AI. This is in part due to the dearth of AI impact data upon which to fit distributions. In this work, we address these gaps in two ways. First, we demonstrate how scenario modelling (grounded in established statistical techniques such as Markov chains, copulas and Monte Carlo simulation) can be used to model AI risk holistically. Second, we show how lookalike distributions from phenomena analogous to AI can be used to estimate AI impacts in the absence of directly observable data. We demonstrate the utility of our methods for benchmarking cumulative AI risk via risk analysis of a logistic scenario simulations.
Infrastructure for AI Agents
Jan 17, 2025



Abstract:Increasingly many AI systems can plan and execute interactions in open-ended environments, such as making phone calls or buying online goods. As developers grow the space of tasks that such AI agents can accomplish, we will need tools both to unlock their benefits and manage their risks. Current tools are largely insufficient because they are not designed to shape how agents interact with existing institutions (e.g., legal and economic systems) or actors (e.g., digital service providers, humans, other AI agents). For example, alignment techniques by nature do not assure counterparties that some human will be held accountable when a user instructs an agent to perform an illegal action. To fill this gap, we propose the concept of agent infrastructure: technical systems and shared protocols external to agents that are designed to mediate and influence their interactions with and impacts on their environments. Agent infrastructure comprises both new tools and reconfigurations or extensions of existing tools. For example, to facilitate accountability, protocols that tie users to agents could build upon existing systems for user authentication, such as OpenID. Just as the Internet relies on infrastructure like HTTPS, we argue that agent infrastructure will be similarly indispensable to ecosystems of agents. We identify three functions for agent infrastructure: 1) attributing actions, properties, and other information to specific agents, their users, or other actors; 2) shaping agents' interactions; and 3) detecting and remedying harmful actions from agents. We propose infrastructure that could help achieve each function, explaining use cases, adoption, limitations, and open questions. Making progress on agent infrastructure can prepare society for the adoption of more advanced agents.
Quantum Fair Machine Learning
Feb 01, 2021

Abstract:In this paper, we inaugurate the field of quantum fair machine learning. We undertake a comparative analysis of differences and similarities between classical and quantum fair machine learning algorithms, specifying how the unique features of quantum computation alter measures, metrics and remediation strategies when quantum algorithms are subject to fairness constraints. We present the first results in quantum fair machine learning by demonstrating the use of Grover's search algorithm to satisfy statistical parity constraints imposed on quantum algorithms. We provide lower-bounds on iterations needed to achieve such statistical parity within $\epsilon$-tolerance. We extend canonical Lipschitz-conditioned individual fairness criteria to the quantum setting using quantum metrics. We examine the consequences for typical measures of fairness in machine learning context when quantum information processing and quantum data are involved. Finally, we propose open questions and research programmes for this new field of interest to researchers in computer science, ethics and quantum computation.
Computability, Complexity, Consistency and Controllability: A Four C's Framework for cross-disciplinary Ethical Algorithm Research
Jan 30, 2021Abstract:The ethical consequences of, constraints upon and regulation of algorithms arguably represent the defining challenges of our age, asking us to reckon with the rise of computational technologies whose potential to radically transforming social and individual orders and identity in unforeseen ways is already being realised. Yet despite the multidisciplinary impact of this algorithmic turn, there remains some way to go in motivating the crossdisciplinary collaboration that is crucial to advancing feasible proposals for the ethical design, implementation and regulation of algorithmic and automated systems. In this work, we provide a framework to assist cross-disciplinary collaboration by presenting a Four C's Framework covering key computational considerations researchers across such diverse fields should consider when approaching these questions: (i) computability, (ii) complexity, (iii) consistency and (iv) controllability. In addition, we provide examples of how insights from ethics, philosophy and population ethics are relevant to and translatable within sciences concerned with the study and design of algorithms. Our aim is to set out a framework which we believe is useful for fostering cross-disciplinary understanding of pertinent issues in ethical algorithmic literature which is relevant considering the feasibility of ethical algorithmic governance, especially the impact of computational constraints upon algorithmic governance.
Quantum Geometric Machine Learning for Quantum Circuits and Control
Jul 07, 2020
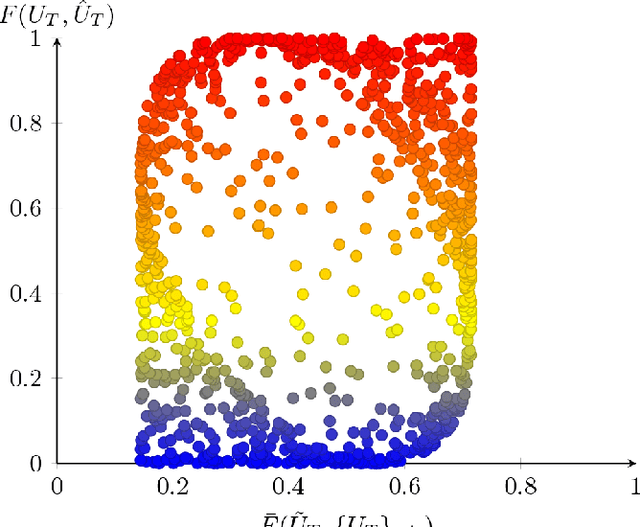
Abstract:The application of machine learning techniques to solve problems in quantum control together with established geometric methods for solving optimisation problems leads naturally to an exploration of how machine learning approaches can be used to enhance geometric approaches to solving problems in quantum information processing. In this work, we review and extend the application of deep learning to quantum geometric control problems. Specifically, we demonstrate enhancements in time-optimal control in the context of quantum circuit synthesis problems by applying novel deep learning algorithms in order to approximate geodesics (and thus minimal circuits) along Lie group manifolds relevant to low-dimensional multi-qubit systems, such as SU(2), SU(4) and SU(8). We demonstrate the superior performance of greybox models, which combine traditional blackbox algorithms with prior domain knowledge of quantum mechanics, as means of learning underlying quantum circuit distributions of interest. Our results demonstrate how geometric control techniques can be used to both (a) verify the extent to which geometrically synthesised quantum circuits lie along geodesic, and thus time-optimal, routes and (b) synthesise those circuits. Our results are of interest to researchers in quantum control and quantum information theory seeking to combine machine learning and geometric techniques for time-optimal control problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge