A Quantum Approach to Synthetic Minority Oversampling Technique (SMOTE)

The paper proposes the Quantum-SMOTE method, a novel solution that uses quantum computing techniques to solve the prevalent problem of class imbalance in machine learning datasets. Quantum-SMOTE, inspired by the Synthetic Minority Oversampling Technique (SMOTE), generates synthetic data points using quantum processes such as swap tests and quantum rotation. The process varies from the conventional SMOTE algorithm's usage of K-Nearest Neighbors (KNN) and Euclidean distances, enabling synthetic instances to be generated from minority class data points without relying on neighbor proximity. The algorithm asserts greater control over the synthetic data generation process by introducing hyperparameters such as rotation angle, minority percentage, and splitting factor, which allow for customization to specific dataset requirements. The approach is tested on a public dataset of TelecomChurn and evaluated alongside two prominent classification algorithms, Random Forest and Logistic Regression, to determine its impact along with varying proportions of synthetic data.

Noise Detection with Spectator Qubits and Quantum Feature Engineering

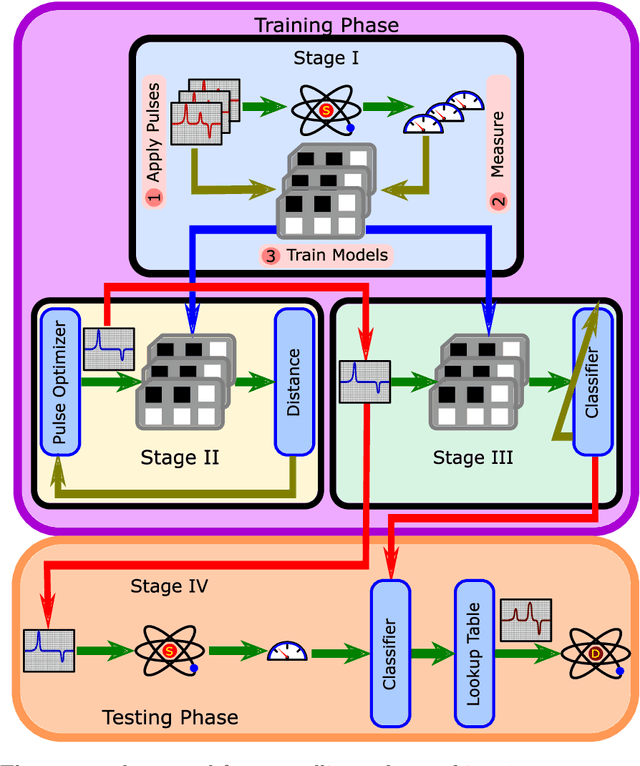
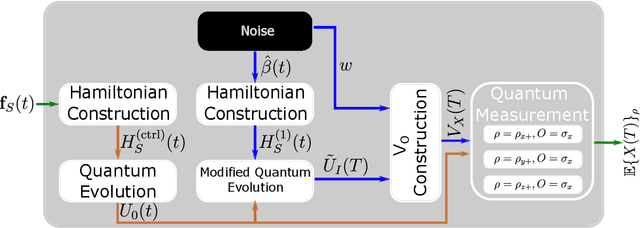
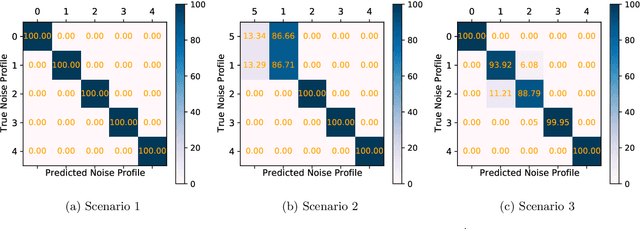
Designing optimal control pulses that drive a noisy qubit to a target state is a challenging and crucial task for quantum engineering. In a situation where the properties of the quantum noise affecting the system are dynamic, a periodic characterization procedure is essential to ensure the models are updated. As a result, the operation of the qubit is disrupted frequently. In this paper, we propose a protocol that addresses this challenge by making use of a spectator qubit to monitor the noise in real-time. We develop a quantum machine-learning-based quantum feature engineering approach for designing the protocol. The complexity of the protocol is front-loaded in a characterization phase, which allow real-time execution during the quantum computations. We present the results of numerical simulations that showcase the favorable performance of the protocol.

Quantum Geometric Machine Learning for Quantum Circuits and Control

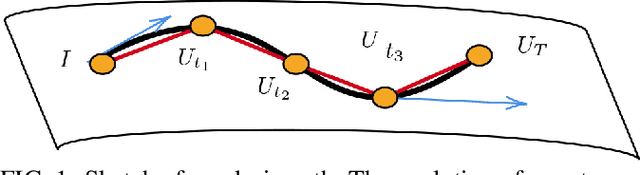
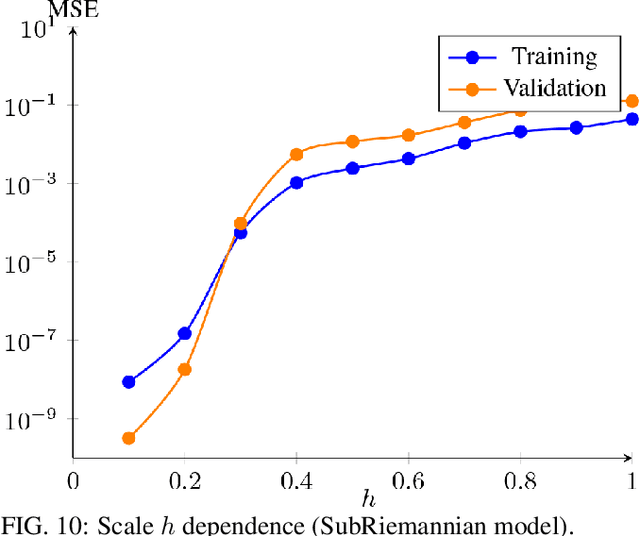
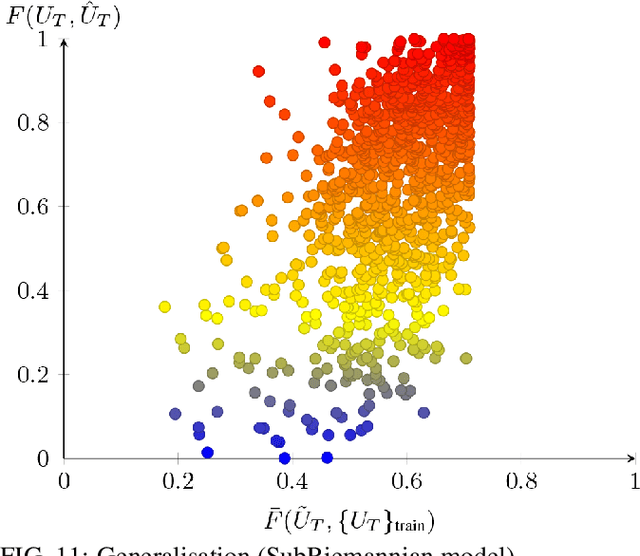
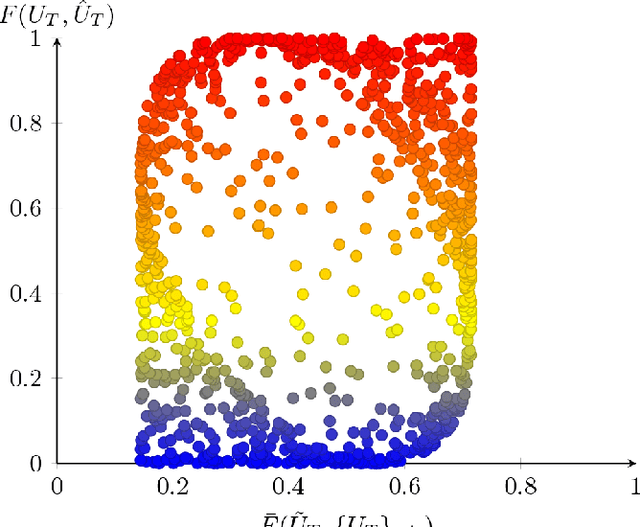
The application of machine learning techniques to solve problems in quantum control together with established geometric methods for solving optimisation problems leads naturally to an exploration of how machine learning approaches can be used to enhance geometric approaches to solving problems in quantum information processing. In this work, we review and extend the application of deep learning to quantum geometric control problems. Specifically, we demonstrate enhancements in time-optimal control in the context of quantum circuit synthesis problems by applying novel deep learning algorithms in order to approximate geodesics (and thus minimal circuits) along Lie group manifolds relevant to low-dimensional multi-qubit systems, such as SU(2), SU(4) and SU(8). We demonstrate the superior performance of greybox models, which combine traditional blackbox algorithms with prior domain knowledge of quantum mechanics, as means of learning underlying quantum circuit distributions of interest. Our results demonstrate how geometric control techniques can be used to both (a) verify the extent to which geometrically synthesised quantum circuits lie along geodesic, and thus time-optimal, routes and (b) synthesise those circuits. Our results are of interest to researchers in quantum control and quantum information theory seeking to combine machine learning and geometric techniques for time-optimal control problems.

Robust Online Hamiltonian Learning

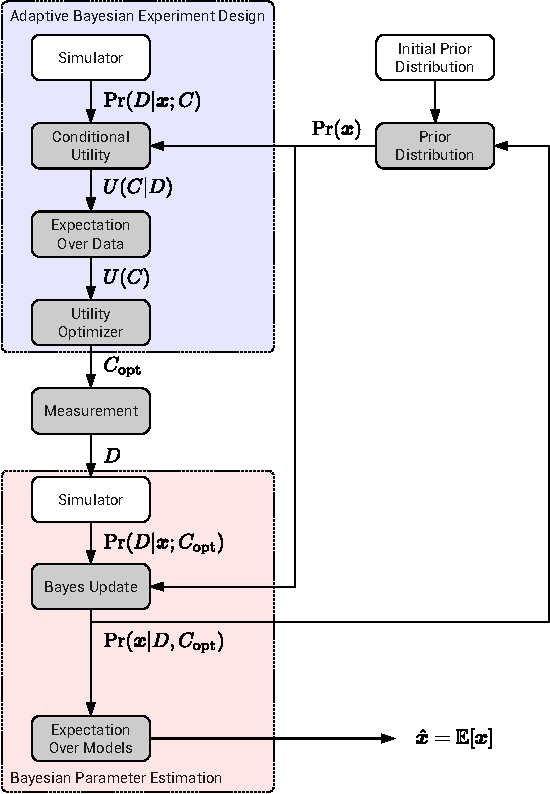
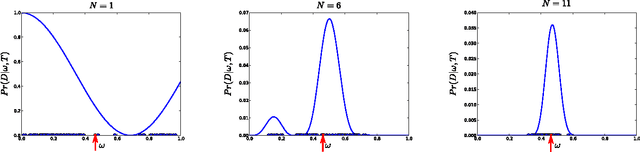
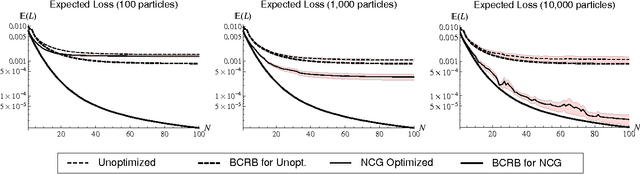
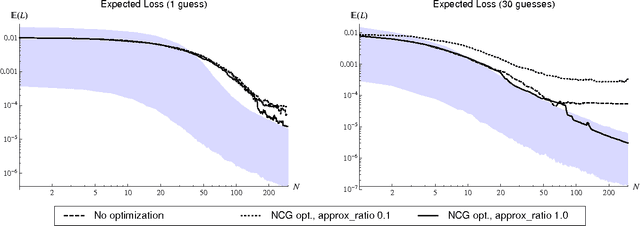
In this work we combine two distinct machine learning methodologies, sequential Monte Carlo and Bayesian experimental design, and apply them to the problem of inferring the dynamical parameters of a quantum system. We design the algorithm with practicality in mind by including parameters that control trade-offs between the requirements on computational and experimental resources. The algorithm can be implemented online (during experimental data collection), avoiding the need for storage and post-processing. Most importantly, our algorithm is capable of learning Hamiltonian parameters even when the parameters change from experiment-to-experiment, and also when additional noise processes are present and unknown. The algorithm also numerically estimates the Cramer-Rao lower bound, certifying its own performance.