Elif Vural
A Unified Analysis of Generalization and Sample Complexity for Semi-Supervised Domain Adaptation
Jul 30, 2025Abstract:Domain adaptation seeks to leverage the abundant label information in a source domain to improve classification performance in a target domain with limited labels. While the field has seen extensive methodological development, its theoretical foundations remain relatively underexplored. Most existing theoretical analyses focus on simplified settings where the source and target domains share the same input space and relate target-domain performance to measures of domain discrepancy. Although insightful, these analyses may not fully capture the behavior of modern approaches that align domains into a shared space via feature transformations. In this paper, we present a comprehensive theoretical study of domain adaptation algorithms based on domain alignment. We consider the joint learning of domain-aligning feature transformations and a shared classifier in a semi-supervised setting. We first derive generalization bounds in a broad setting, in terms of covering numbers of the relevant function classes. We then extend our analysis to characterize the sample complexity of domain-adaptive neural networks employing maximum mean discrepancy (MMD) or adversarial objectives. Our results rely on a rigorous analysis of the covering numbers of these architectures. We show that, for both MMD-based and adversarial models, the sample complexity admits an upper bound that scales quadratically with network depth and width. Furthermore, our analysis suggests that in semi-supervised settings, robustness to limited labeled target data can be achieved by scaling the target loss proportionally to the square root of the number of labeled target samples. Experimental evaluation in both shallow and deep settings lends support to our theoretical findings.
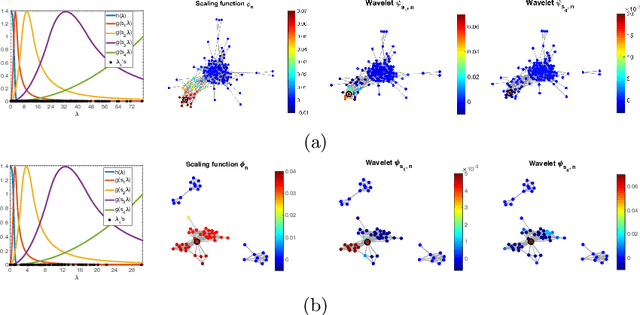
Graph Signal Inference by Learning Narrowband Spectral Kernels
Feb 19, 2025Abstract:While a common assumption in graph signal analysis is the smoothness of the signals or the band-limitedness of their spectrum, in many instances the spectrum of real graph data may be concentrated at multiple regions of the spectrum, possibly including mid-to-high-frequency components. In this work, we propose a novel graph signal model where the signal spectrum is represented through the combination of narrowband kernels in the graph frequency domain. We then present an algorithm that jointly learns the model by optimizing the kernel parameters and the signal representation coefficients from a collection of graph signals. Our problem formulation has the flexibility of permitting the incorporation of signals possibly acquired on different graphs into the learning algorithm. We then theoretically study the signal reconstruction performance of the proposed method, by also elaborating on when joint learning on multiple graphs is preferable to learning an individual model on each graph. Experimental results on several graph data sets shows that the proposed method offers quite satisfactory signal interpolation accuracy in comparison with a variety of reference approaches in the literature.
Downlink CCM Estimation via Representation Learning with Graph Regularization
Jul 26, 2024Abstract:In this paper, we propose an algorithm for downlink (DL) channel covariance matrix (CCM) estimation for frequency division duplexing (FDD) massive multiple-input multiple-output (MIMO) communication systems with base station (BS) possessing a uniform linear array (ULA) antenna structure. We make use of the inherent similarity between the uplink (UL) CCM and the DL CCM due to angular reciprocity. We consider a setting where the UL CCM is mapped to DL CCM by a mapping function. We first present a theoretical error analysis of learning a nonlinear embedding by constructing a mapping function, which points to the importance of the Lipschitz regularity of the mapping function for achieving high estimation performance. Then, based on the theoretical ground, we propose a representation learning algorithm as a solution for the estimation problem, where Gaussian RBF kernel interpolators are chosen to map UL CCMs to their DL counterparts. The proposed algorithm is based on the optimization of an objective function that fits a regression model between the DL CCM and UL CCM samples in the training dataset and preserves the local geometric structure of the data in the UL CCM space, while explicitly regulating the Lipschitz continuity of the mapping function in light of our theoretical findings. The proposed algorithm surpasses benchmark methods in terms of three error metrics as shown by simulations.
Locally Stationary Graph Processes
Sep 04, 2023Abstract:Stationary graph process models are commonly used in the analysis and inference of data sets collected on irregular network topologies. While most of the existing methods represent graph signals with a single stationary process model that is globally valid on the entire graph, in many practical problems, the characteristics of the process may be subject to local variations in different regions of the graph. In this work, we propose a locally stationary graph process (LSGP) model that aims to extend the classical concept of local stationarity to irregular graph domains. We characterize local stationarity by expressing the overall process as the combination of a set of component processes such that the extent to which the process adheres to each component varies smoothly over the graph. We propose an algorithm for computing LSGP models from realizations of the process, and also study the approximation of LSGPs locally with WSS processes. Experiments on signal interpolation problems show that the proposed process model provides accurate signal representations competitive with the state of the art.
Learning Graph ARMA Processes from Time-Vertex Spectra
Feb 14, 2023Abstract:The modeling of time-varying graph signals as stationary time-vertex stochastic processes permits the inference of missing signal values by efficiently employing the correlation patterns of the process across different graph nodes and time instants. In this study, we first propose an algorithm for computing graph autoregressive moving average (graph ARMA) processes based on learning the joint time-vertex power spectral density of the process from its incomplete realizations. Our solution relies on first roughly estimating the joint spectrum of the process from partially observed realizations and then refining this estimate by projecting it onto the spectrum manifold of the ARMA process. We then present a theoretical analysis of the sample complexity of learning graph ARMA processes. Experimental results show that the proposed approach achieves improvement in the time-vertex signal estimation performance in comparison with reference approaches in the literature.
Learning Multi-Modal Nonlinear Embeddings: Performance Bounds and an Algorithm
Jun 03, 2020

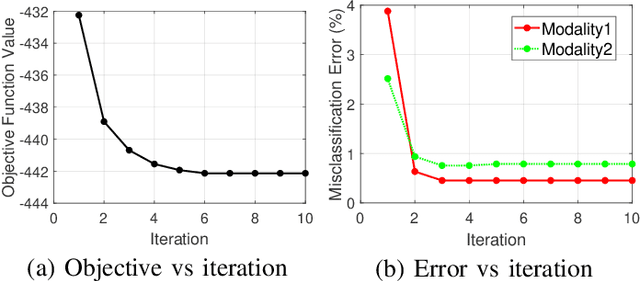
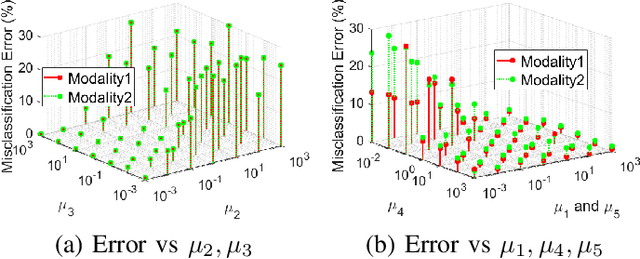
Abstract:While many approaches exist in the literature to learn representations for data collections in multiple modalities, the generalizability of the learnt representations to previously unseen data is a largely overlooked subject. In this work, we first present a theoretical analysis of learning multi-modal nonlinear embeddings in a supervised setting. Our performance bounds indicate that for successful generalization in multi-modal classification and retrieval problems, the regularity of the interpolation functions extending the embedding to the whole data space is as important as the between-class separation and cross-modal alignment criteria. We then propose a multi-modal nonlinear representation learning algorithm that is motivated by these theoretical findings, where the embeddings of the training samples are optimized jointly with the Lipschitz regularity of the interpolators. Experimental comparison to recent multi-modal and single-modal learning algorithms suggests that the proposed method yields promising performance in multi-modal image classification and cross-modal image-text retrieval applications.
Graph Domain Adaptation with Localized Graph Signal Representations
Nov 07, 2019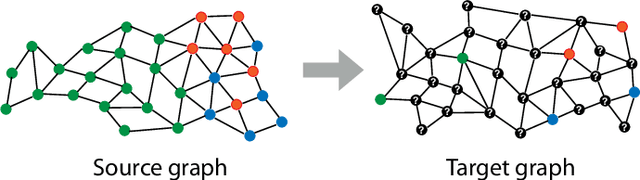
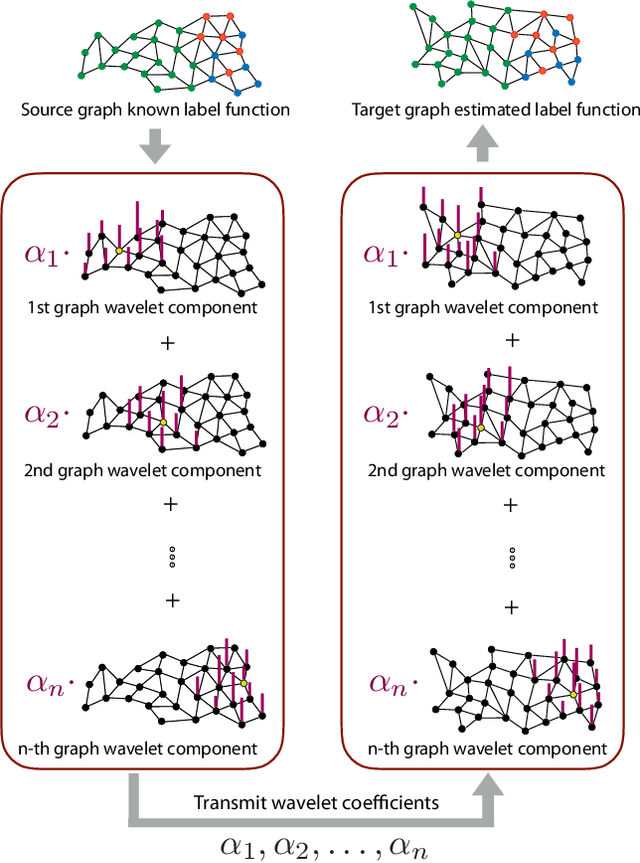
Abstract:In this paper we propose a domain adaptation algorithm designed for graph domains. Given a source graph with many labeled nodes and a target graph with few or no labeled nodes, we aim to estimate the target labels by making use of the similarity between the characteristics of the variation of the label functions on the two graphs. Our assumption about the source and the target domains is that the local behaviour of the label function, such as its spread and speed of variation on the graph, bears resemblance between the two graphs. We estimate the unknown target labels by solving an optimization problem where the label information is transferred from the source graph to the target graph based on the prior that the projections of the label functions onto localized graph bases be similar between the source and the target graphs. In order to efficiently capture the local variation of the label functions on the graphs, spectral graph wavelets are used as the graph bases. Experimentation on various data sets shows that the proposed method yields quite satisfactory classification accuracy compared to reference domain adaptation methods.
Mask Combination of Multi-layer Graphs for Global Structure Inference
Oct 22, 2019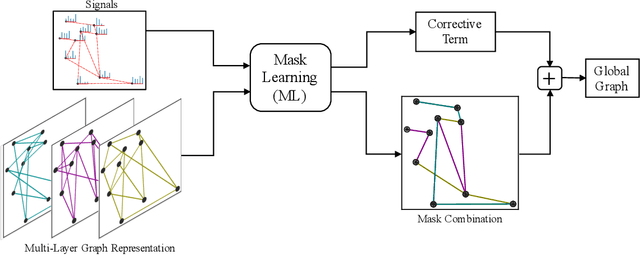
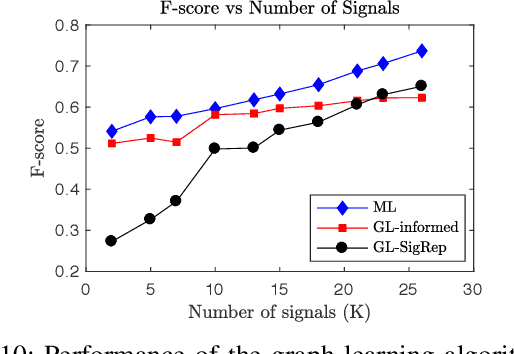
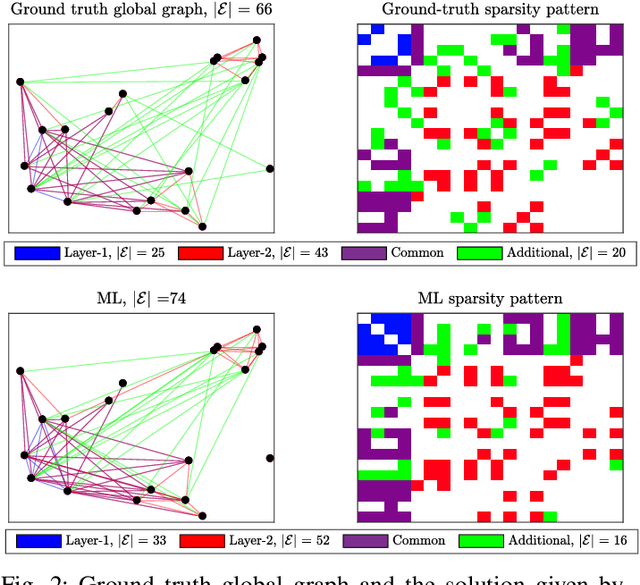
Abstract:Structure inference is an important task for network data processing and analysis in data science. In recent years, quite a few approaches have been developed to learn the graph structure underlying a set of observations captured in a data space. Although real world data is often acquired in settings where relationships are influenced by a priori known rules, this domain knowledge is still not well exploited in structure inference problems. In this paper, we identify the structure of signals defined in a data space whose inner relationships are encoded by multi-layer graphs. We aim at properly exploiting the information originating from each layer to infer the global structure underlying the signals. We thus present a novel method for combining the multiple graphs into a global graph using mask matrices, which are estimated through an optimization problem that accommodates the multi-layer graph information and a signal representation model. The proposed mask combination method also estimates the contribution of each graph layer in the structure of signals. The experiments conducted both on synthetic and real world data suggest that integrating the multi-layer graph representation of the data in the structure inference framework enhances the learning procedure considerably by adapting to the quality and the quantity of the input data
Domain Adaptation on Graphs by Learning Graph Topologies: Theoretical Analysis and an Algorithm
Dec 17, 2018


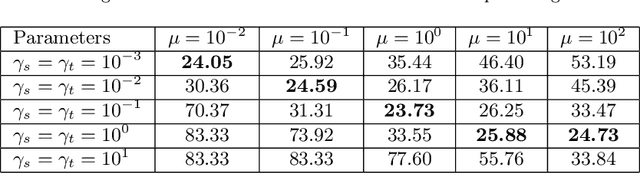
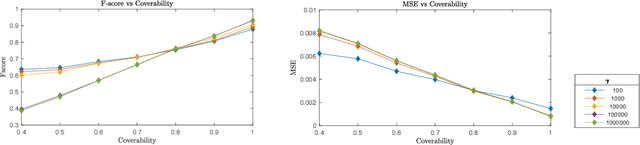
Abstract:Traditional machine learning algorithms assume that the training and test data have the same distribution, while this assumption can be easily violated in real applications. Learning by taking into account the changes in the data distribution is called domain adaptation. In this work, we treat the domain adaptation problem in a graph setting. We consider a source and a target data graph that are constructed with samples drawn from a source and a target data manifold. We study the problem of estimating the unknown labels on the target graph by employing the label information in the source graph and the similarity between the two graphs. We particularly focus on a setting where the target label function is learnt such that its spectrum (frequency content when regarded as a graph signal) is similar to that of the source label function. We first present an overview of the recent field of graph signal processing and introduce concepts such as the Fourier transform on graphs. We then propose a theoretical analysis of domain adaptation over graphs, and present performance bounds relating the target classification error to the properties of the graph topologies and the manifold geometries. Finally, we propose a graph domain adaptation algorithm inspired by our theoretical findings, which estimates the label functions while learning the source and target graph topologies at the same time. Experiments on synthetic and real data sets suggest that the proposed method outperforms baseline approaches.
Nonlinear Supervised Dimensionality Reduction via Smooth Regular Embeddings
May 28, 2018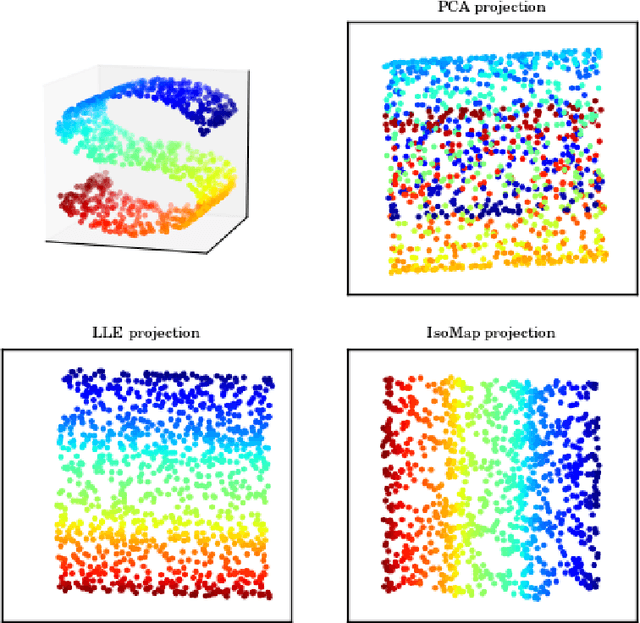
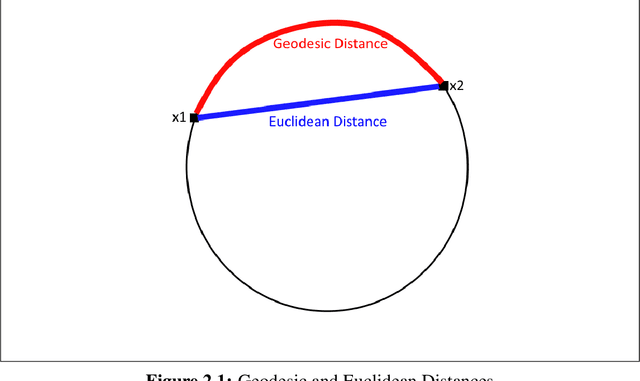
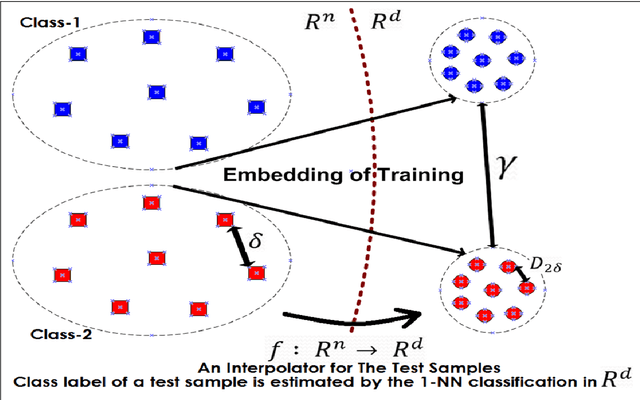

Abstract:The recovery of the intrinsic geometric structures of data collections is an important problem in data analysis. Supervised extensions of several manifold learning approaches have been proposed in the recent years. Meanwhile, existing methods primarily focus on the embedding of the training data, and the generalization of the embedding to initially unseen test data is rather ignored. In this work, we build on recent theoretical results on the generalization performance of supervised manifold learning algorithms. Motivated by these performance bounds, we propose a supervised manifold learning method that computes a nonlinear embedding while constructing a smooth and regular interpolation function that extends the embedding to the whole data space in order to achieve satisfactory generalization. The embedding and the interpolator are jointly learnt such that the Lipschitz regularity of the interpolator is imposed while ensuring the separation between different classes. Experimental results on several image data sets show that the proposed method outperforms traditional classifiers and the supervised dimensionality reduction algorithms in comparison in terms of classification accuracy in most settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge