Downlink CCM Estimation via Representation Learning with Graph Regularization

In this paper, we propose an algorithm for downlink (DL) channel covariance matrix (CCM) estimation for frequency division duplexing (FDD) massive multiple-input multiple-output (MIMO) communication systems with base station (BS) possessing a uniform linear array (ULA) antenna structure. We make use of the inherent similarity between the uplink (UL) CCM and the DL CCM due to angular reciprocity. We consider a setting where the UL CCM is mapped to DL CCM by a mapping function. We first present a theoretical error analysis of learning a nonlinear embedding by constructing a mapping function, which points to the importance of the Lipschitz regularity of the mapping function for achieving high estimation performance. Then, based on the theoretical ground, we propose a representation learning algorithm as a solution for the estimation problem, where Gaussian RBF kernel interpolators are chosen to map UL CCMs to their DL counterparts. The proposed algorithm is based on the optimization of an objective function that fits a regression model between the DL CCM and UL CCM samples in the training dataset and preserves the local geometric structure of the data in the UL CCM space, while explicitly regulating the Lipschitz continuity of the mapping function in light of our theoretical findings. The proposed algorithm surpasses benchmark methods in terms of three error metrics as shown by simulations.

Quasi-Newton Detection in One-Bit Pseudo-Randomly Quantized Wideband Massive MIMO Systems

Using low-resolution analog-to-digital converters (ADCs) is a valuable solution to decrease power consumption and cost in massive MIMO systems. Previous studies show that the performance gap between low and high-resolution systems gets more prominent as the signal-to-noise ratio (SNR) increases since the detection performance starts to saturate at some point due to the stochastic resonance (SR) phenomenon. In our previous work, we proposed new quantization and detection schemes for one-bit massive MIMO systems operating under frequency-flat fading. This paper offers a new frequency domain equalization (FDE) scheme that can work with the previously proposed pseudo-random quantization (PRQ) scheme to mitigate the effects of SR to support high-order modulation schemes such as $64$-QAM and $256$-QAM. Our equalizer is based on a projected quasi-Newton method for one-bit uplink massive MIMO systems applicable for orthogonal frequency division multiplexing (OFDM) and single carrier (SC) transmission under frequency-selective fading. The proposed low-complexity detector can outperform the benchmark detector from the literature with very similar complexity. We analyze the effects of PRQ under frequency-selective fading for different scenarios and show that the PRQ scheme can close the performance gap between SC and OFDM systems by simulations.

Pseudo-Random Quantization Based Two-Stage Detection in One-Bit Massive MIMO Systems

Utilizing low-resolution analog-to-digital converters (ADCs) in uplink massive multiple-input multiple-output (MIMO) systems is a practical solution to decrease power consumption. The performance gap between the low and high-resolution systems is small at low signal-to-noise ratio (SNR) regimes. However, at high SNR and with high modulation orders, the achievable rate saturates after a finite SNR value due to the stochastic resonance (SR) phenomenon. This paper proposes a novel pseudo-random quantization (PRQ) scheme by modifying the quantization thresholds that can help compensate for the effects of SR and makes communication with high-order modulation schemes such as $1024$-QAM in one-bit quantized uplink massive MIMO systems possible. Moreover, modified linear detectors for non-zero threshold quantization are derived, and a two-stage uplink detector for single-carrier (SC) multi-user systems is proposed. The first stage is an iterative method called Boxed Newton Detector (BND) that utilizes Newton's Method to maximize the log-likelihood with box constraints. The second stage, Nearest Codeword Detector (NCD), exploits the first stage solution and creates a small set of most likely candidates based on sign constraints to increase detection performance. The proposed two-stage method with PRQ outperforms the state-of-the-art detectors from the literature with comparable complexity while supporting high-order modulation schemes.

A Theoretical Performance Bound for Joint Beamformer Design of Wireless Fronthaul and Access Links in Downlink C-RAN

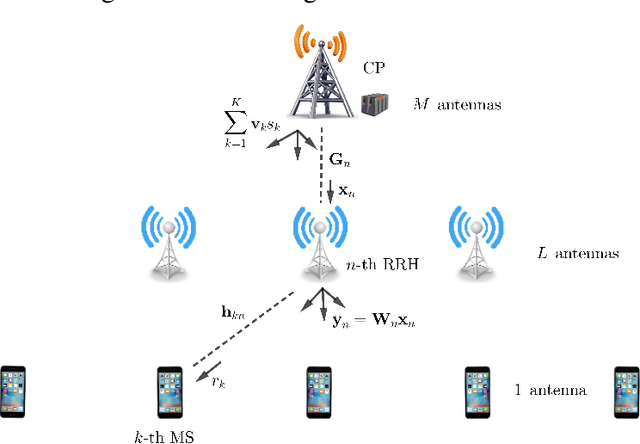
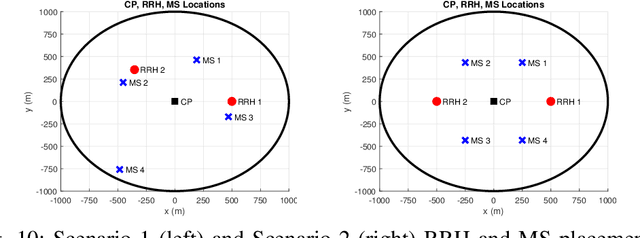
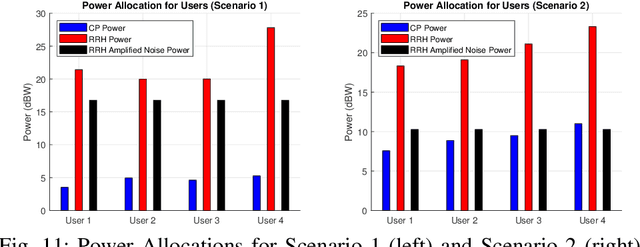
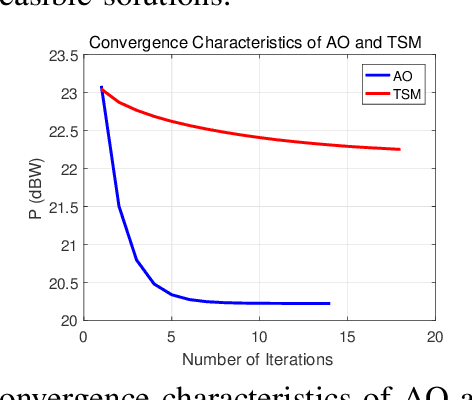
It is known that data rates in standard cellular networks are limited due to inter-cell interference. An effective solution of this problem is to use the multi-cell cooperation idea. In Cloud Radio Access Network (C-RAN), which is a candidate solution in 5G and future communication networks, cooperation is applied by means of central processors (CPs) connected to simple remote radio heads with finite capacity fronthaul links. In this study, we consider a downlink C-RAN with a wireless fronthaul and aim to minimize total power spent by jointly designing beamformers for fronthaul and access links. We consider the case where perfect channel state information is not available in the CP. We first derive a novel theoretical performance bound for the problem defined. Then we propose four algorithms with different complexities to show the tightness of the bound. The first two algorithms apply successive convex optimizations with semi-definite relaxation idea where other two are adapted from well-known beamforming design methods. The detailed simulations under realistic channel conditions show that as the complexity of the algorithm increases, the corresponding performance becomes closer to the bound.

Beamformer Design with Smooth Constraint-Free Approximation in Downlink Cloud Radio Access Networks

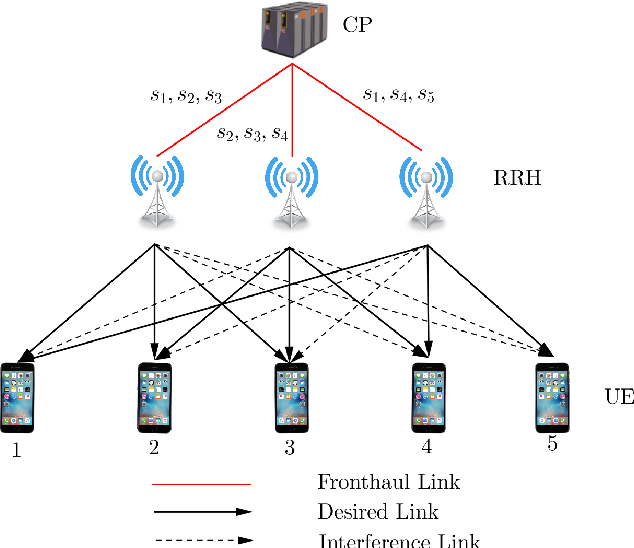
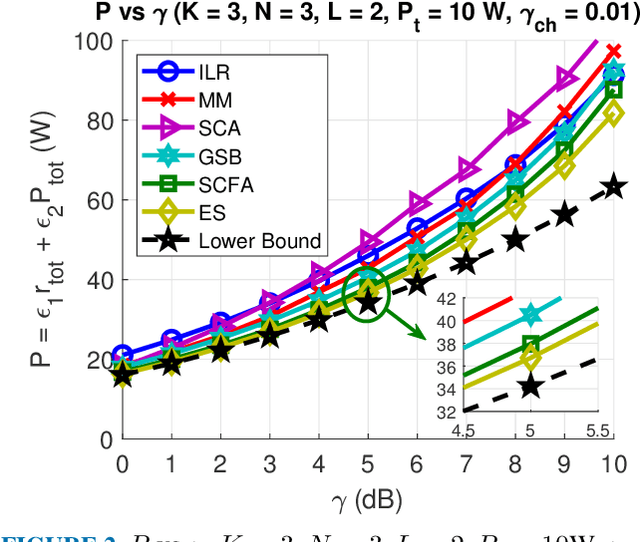
It is known that data rates in standard cellular networks are limited due to inter-cell interference. An effective solution of this problem is to use the multi-cell cooperation idea. In Cloud Radio Access Network, which is a candidate solution in 5G and beyond, cooperation is applied by means of central processors (CPs) connected to simple remote radio heads with finite capacity fronthaul links. In this study, we consider a downlink scenario and aim to minimize total power spent by designing beamformers. We consider the case where perfect channel state information is not available in the CP. The original problem includes discontinuous terms with many constraints. We propose a novel method which transforms the problem into a smooth constraint-free form and a solution is found by the gradient descent approach. As a comparison, we consider the optimal method solving an extensive number of convex sub-problems, a known heuristic search algorithm and some sparse solution techniques. Heuristic search methods find a solution by solving a subset of all possible convex sub-problems. Sparse techniques apply some norm approximation ($\ell_0/\ell_1, \ell_0/\ell_2$) or convex approximation to make the objective function more tractable. We also derive a theoretical performance bound in order to observe how far the proposed method performs off the optimal method when running the optimal method is prohibitive due to computational complexity. Detailed simulations show that the performance of the proposed method is close to the optimal one, and it outperforms other methods analyzed.