Eylem Tugce Guneyi
Learning Graph ARMA Processes from Time-Vertex Spectra
Feb 14, 2023Abstract:The modeling of time-varying graph signals as stationary time-vertex stochastic processes permits the inference of missing signal values by efficiently employing the correlation patterns of the process across different graph nodes and time instants. In this study, we first propose an algorithm for computing graph autoregressive moving average (graph ARMA) processes based on learning the joint time-vertex power spectral density of the process from its incomplete realizations. Our solution relies on first roughly estimating the joint spectrum of the process from partially observed realizations and then refining this estimate by projecting it onto the spectrum manifold of the ARMA process. We then present a theoretical analysis of the sample complexity of learning graph ARMA processes. Experimental results show that the proposed approach achieves improvement in the time-vertex signal estimation performance in comparison with reference approaches in the literature.
Graph Domain Adaptation with Localized Graph Signal Representations
Nov 07, 2019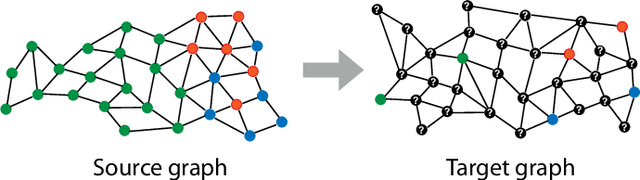
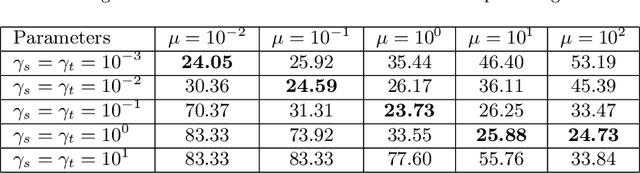
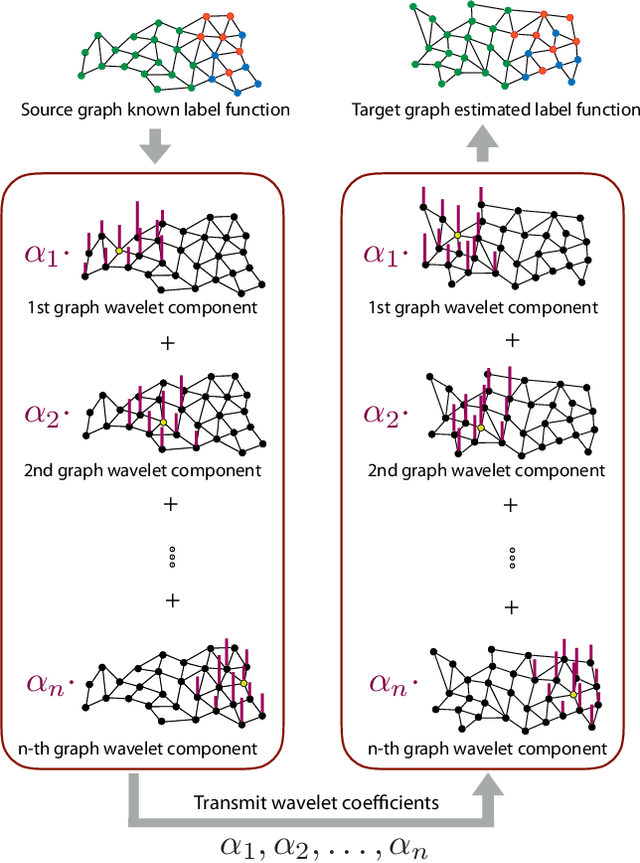
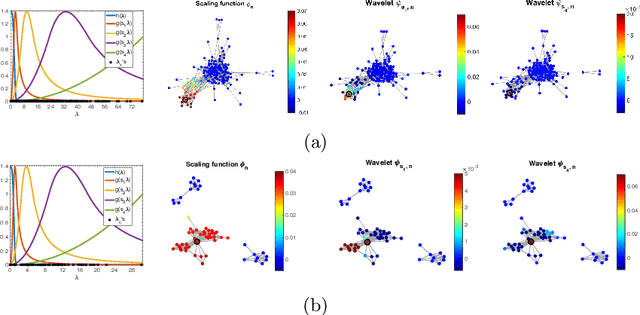
Abstract:In this paper we propose a domain adaptation algorithm designed for graph domains. Given a source graph with many labeled nodes and a target graph with few or no labeled nodes, we aim to estimate the target labels by making use of the similarity between the characteristics of the variation of the label functions on the two graphs. Our assumption about the source and the target domains is that the local behaviour of the label function, such as its spread and speed of variation on the graph, bears resemblance between the two graphs. We estimate the unknown target labels by solving an optimization problem where the label information is transferred from the source graph to the target graph based on the prior that the projections of the label functions onto localized graph bases be similar between the source and the target graphs. In order to efficiently capture the local variation of the label functions on the graphs, spectral graph wavelets are used as the graph bases. Experimentation on various data sets shows that the proposed method yields quite satisfactory classification accuracy compared to reference domain adaptation methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge