Domain Adaptation on Graphs by Learning Graph Topologies: Theoretical Analysis and an Algorithm

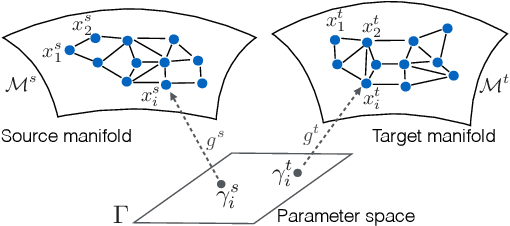
Traditional machine learning algorithms assume that the training and test data have the same distribution, while this assumption can be easily violated in real applications. Learning by taking into account the changes in the data distribution is called domain adaptation. In this work, we treat the domain adaptation problem in a graph setting. We consider a source and a target data graph that are constructed with samples drawn from a source and a target data manifold. We study the problem of estimating the unknown labels on the target graph by employing the label information in the source graph and the similarity between the two graphs. We particularly focus on a setting where the target label function is learnt such that its spectrum (frequency content when regarded as a graph signal) is similar to that of the source label function. We first present an overview of the recent field of graph signal processing and introduce concepts such as the Fourier transform on graphs. We then propose a theoretical analysis of domain adaptation over graphs, and present performance bounds relating the target classification error to the properties of the graph topologies and the manifold geometries. Finally, we propose a graph domain adaptation algorithm inspired by our theoretical findings, which estimates the label functions while learning the source and target graph topologies at the same time. Experiments on synthetic and real data sets suggest that the proposed method outperforms baseline approaches.