Propagation on Multi-relational Graphs for Node Regression

Recent years have witnessed a rise in real-world data captured with rich structural information that can be conveniently depicted by multi-relational graphs. While inference of continuous node features across a simple graph is rather under-studied by the current relational learning research, we go one step further and focus on node regression problem on multi-relational graphs. We take inspiration from the well-known label propagation algorithm aiming at completing categorical features across a simple graph and propose a novel propagation framework for completing missing continuous features at the nodes of a multi-relational and directed graph. Our multi-relational propagation algorithm is composed of iterative neighborhood aggregations which originate from a relational local generative model. Our findings show the benefit of exploiting the multi-relational structure of the data in several node regression scenarios in different settings.

Node Attribute Completion in Knowledge Graphs with Multi-Relational Propagation

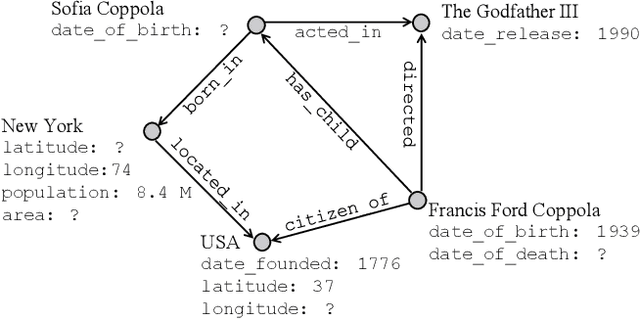
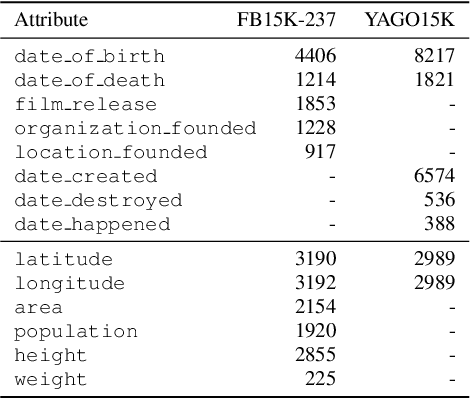
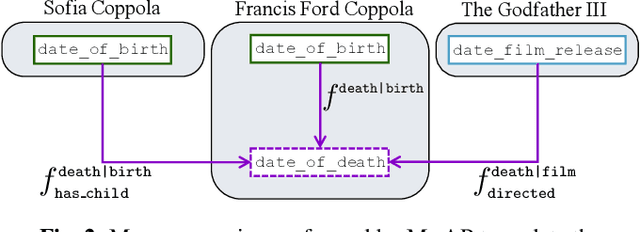
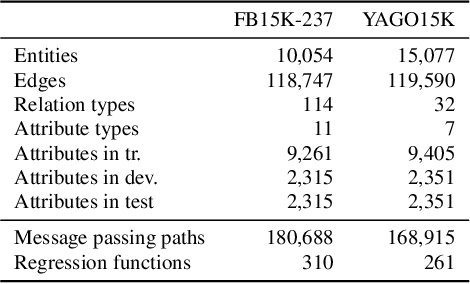
The existing literature on knowledge graph completion mostly focuses on the link prediction task. However, knowledge graphs have an additional incompleteness problem: their nodes possess numerical attributes, whose values are often missing. Our approach, denoted as MrAP, imputes the values of missing attributes by propagating information across the multi-relational structure of a knowledge graph. It employs regression functions for predicting one node attribute from another depending on the relationship between the nodes and the type of the attributes. The propagation mechanism operates iteratively in a message passing scheme that collects the predictions at every iteration and updates the value of the node attributes. Experiments over two benchmark datasets show the effectiveness of our approach.

Mask Combination of Multi-layer Graphs for Global Structure Inference

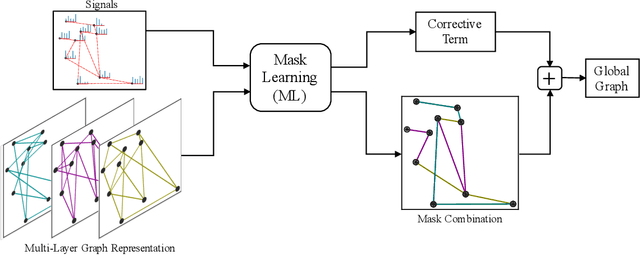
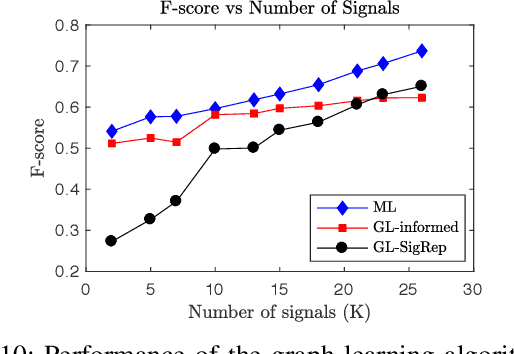
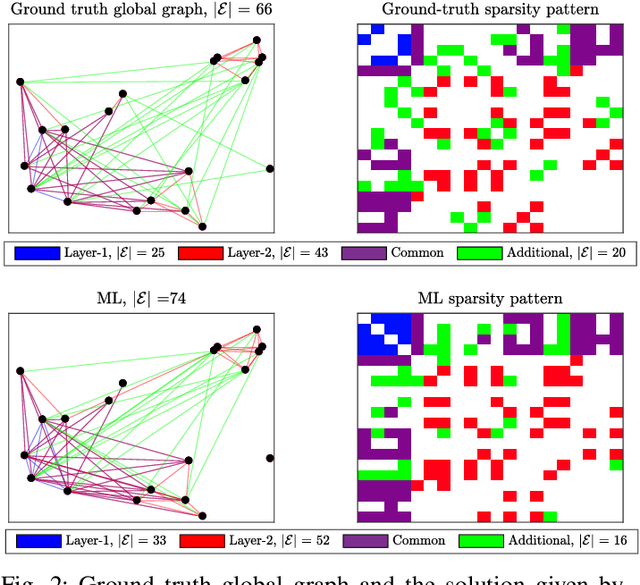
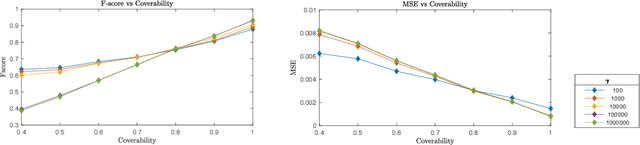
Structure inference is an important task for network data processing and analysis in data science. In recent years, quite a few approaches have been developed to learn the graph structure underlying a set of observations captured in a data space. Although real world data is often acquired in settings where relationships are influenced by a priori known rules, this domain knowledge is still not well exploited in structure inference problems. In this paper, we identify the structure of signals defined in a data space whose inner relationships are encoded by multi-layer graphs. We aim at properly exploiting the information originating from each layer to infer the global structure underlying the signals. We thus present a novel method for combining the multiple graphs into a global graph using mask matrices, which are estimated through an optimization problem that accommodates the multi-layer graph information and a signal representation model. The proposed mask combination method also estimates the contribution of each graph layer in the structure of signals. The experiments conducted both on synthetic and real world data suggest that integrating the multi-layer graph representation of the data in the structure inference framework enhances the learning procedure considerably by adapting to the quality and the quantity of the input data