On Acceleration of Gradient-Based Empirical Risk Minimization using Local Polynomial Regression

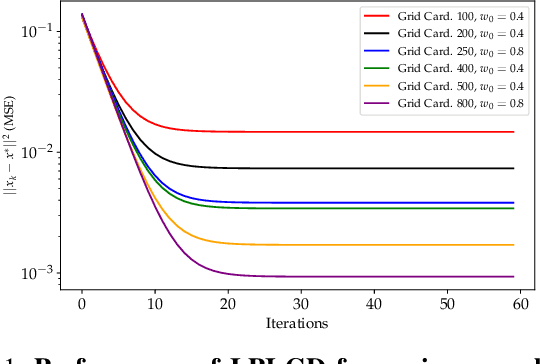
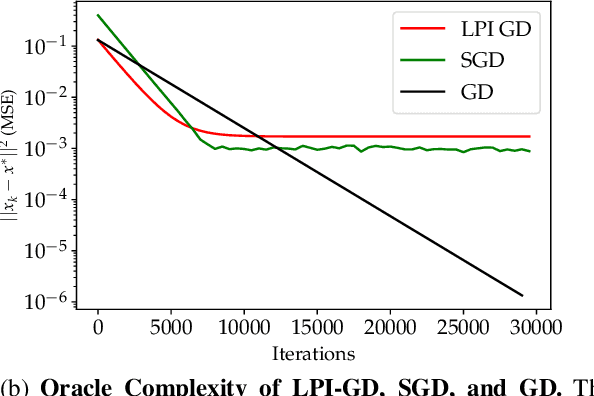
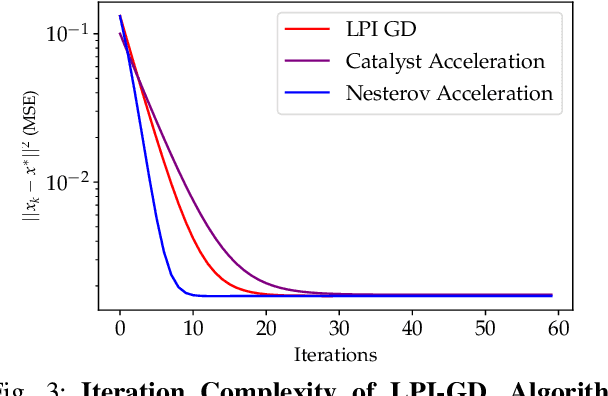
We study the acceleration of the Local Polynomial Interpolation-based Gradient Descent method (LPI-GD) recently proposed for the approximate solution of empirical risk minimization problems (ERM). We focus on loss functions that are strongly convex and smooth with condition number $\sigma$. We additionally assume the loss function is $\eta$-H\"older continuous with respect to the data. The oracle complexity of LPI-GD is $\tilde{O}\left(\sigma m^d \log(1/\varepsilon)\right)$ for a desired accuracy $\varepsilon$, where $d$ is the dimension of the parameter space, and $m$ is the cardinality of an approximation grid. The factor $m^d$ can be shown to scale as $O((1/\varepsilon)^{d/2\eta})$. LPI-GD has been shown to have better oracle complexity than gradient descent (GD) and stochastic gradient descent (SGD) for certain parameter regimes. We propose two accelerated methods for the ERM problem based on LPI-GD and show an oracle complexity of $\tilde{O}\left(\sqrt{\sigma} m^d \log(1/\varepsilon)\right)$. Moreover, we provide the first empirical study on local polynomial interpolation-based gradient methods and corroborate that LPI-GD has better performance than GD and SGD in some scenarios, and the proposed methods achieve acceleration.

Manifold Topology Divergence: a Framework for Comparing Data Manifolds

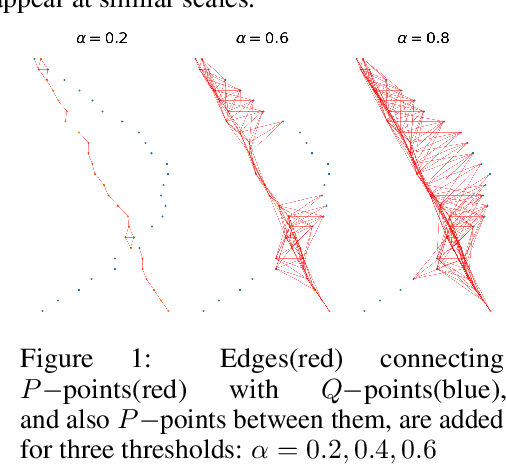
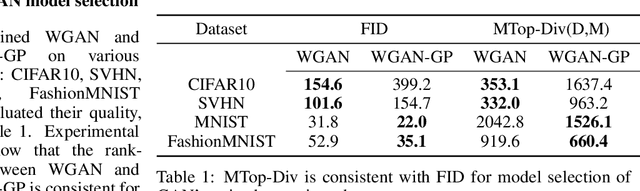
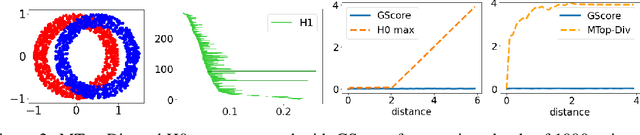
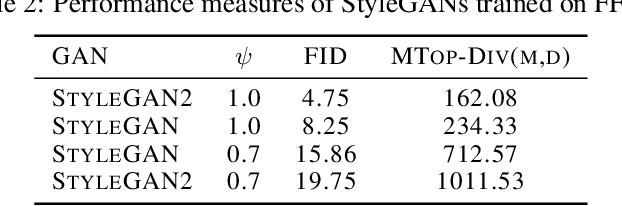
We develop a framework for comparing data manifolds, aimed, in particular, towards the evaluation of deep generative models. We describe a novel tool, Cross-Barcode(P,Q), that, given a pair of distributions in a high-dimensional space, tracks multiscale topology spacial discrepancies between manifolds on which the distributions are concentrated. Based on the Cross-Barcode, we introduce the Manifold Topology Divergence score (MTop-Divergence) and apply it to assess the performance of deep generative models in various domains: images, 3D-shapes, time-series, and on different datasets: MNIST, Fashion MNIST, SVHN, CIFAR10, FFHQ, chest X-ray images, market stock data, ShapeNet. We demonstrate that the MTop-Divergence accurately detects various degrees of mode-dropping, intra-mode collapse, mode invention, and image disturbance. Our algorithm scales well (essentially linearly) with the increase of the dimension of the ambient high-dimensional space. It is one of the first TDA-based practical methodologies that can be applied universally to datasets of different sizes and dimensions, including the ones on which the most recent GANs in the visual domain are trained. The proposed method is domain agnostic and does not rely on pre-trained networks.