Grigorii Sotnikov
Manifold Topology Divergence: a Framework for Comparing Data Manifolds
Jun 08, 2021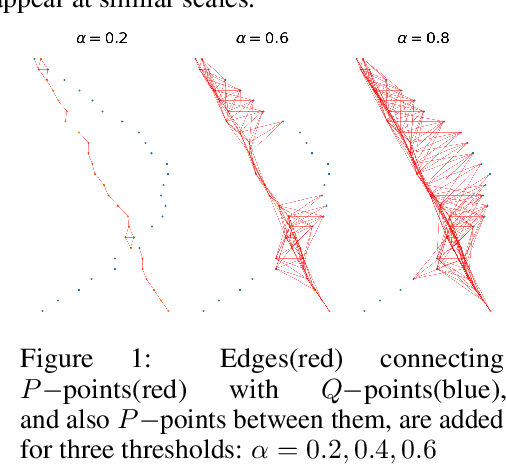
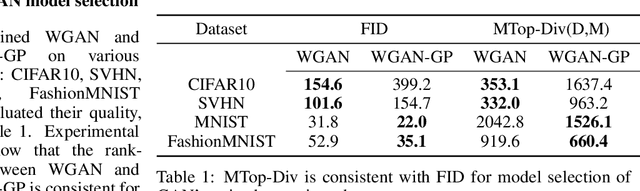
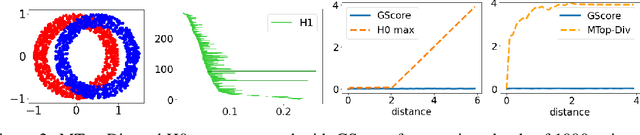
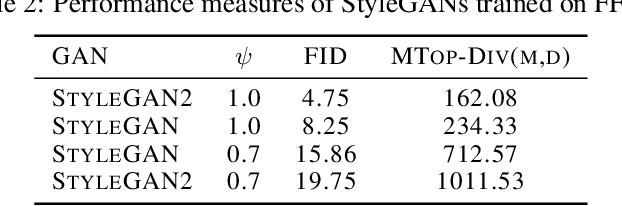
Abstract:We develop a framework for comparing data manifolds, aimed, in particular, towards the evaluation of deep generative models. We describe a novel tool, Cross-Barcode(P,Q), that, given a pair of distributions in a high-dimensional space, tracks multiscale topology spacial discrepancies between manifolds on which the distributions are concentrated. Based on the Cross-Barcode, we introduce the Manifold Topology Divergence score (MTop-Divergence) and apply it to assess the performance of deep generative models in various domains: images, 3D-shapes, time-series, and on different datasets: MNIST, Fashion MNIST, SVHN, CIFAR10, FFHQ, chest X-ray images, market stock data, ShapeNet. We demonstrate that the MTop-Divergence accurately detects various degrees of mode-dropping, intra-mode collapse, mode invention, and image disturbance. Our algorithm scales well (essentially linearly) with the increase of the dimension of the ambient high-dimensional space. It is one of the first TDA-based practical methodologies that can be applied universally to datasets of different sizes and dimensions, including the ones on which the most recent GANs in the visual domain are trained. The proposed method is domain agnostic and does not rely on pre-trained networks.
Aligning Latent and Image Spaces to Connect the Unconnectable
Apr 14, 2021



Abstract:In this work, we develop a method to generate infinite high-resolution images with diverse and complex content. It is based on a perfectly equivariant generator with synchronous interpolations in the image and latent spaces. Latent codes, when sampled, are positioned on the coordinate grid, and each pixel is computed from an interpolation of the nearby style codes. We modify the AdaIN mechanism to work in such a setup and train the generator in an adversarial setting to produce images positioned between any two latent vectors. At test time, this allows for generating complex and diverse infinite images and connecting any two unrelated scenes into a single arbitrarily large panorama. Apart from that, we introduce LHQ: a new dataset of \lhqsize high-resolution nature landscapes. We test the approach on LHQ, LSUN Tower and LSUN Bridge and outperform the baselines by at least 4 times in terms of quality and diversity of the produced infinite images. The project page is located at https://universome.github.io/alis.
Topological obstructions in neural networks learning
Dec 31, 2020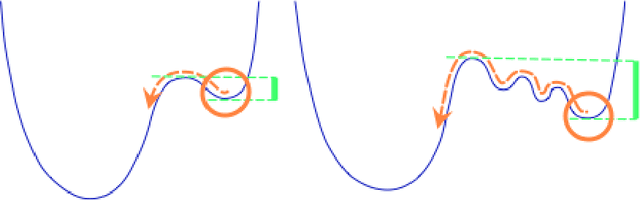
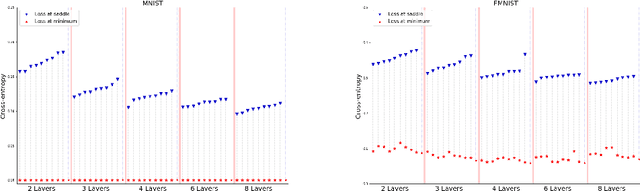
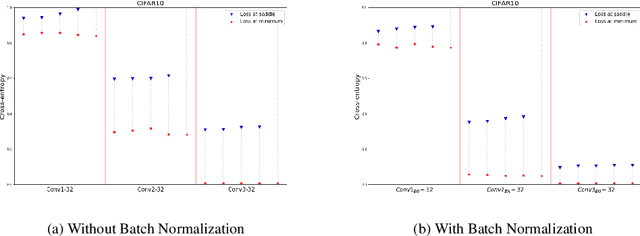
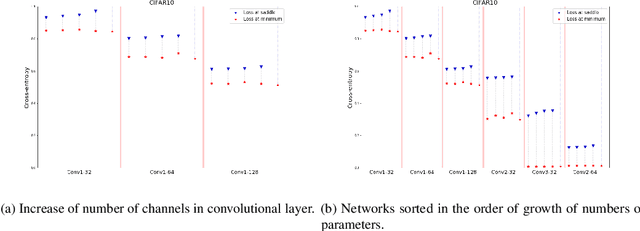
Abstract:We apply methods of topological data analysis to loss functions to gain insights on learning of deep neural networks and their generalization properties. We study global properties of the loss function gradient flow. We use topological data analysis of the loss function and its Morse complex to relate local behavior along gradient trajectories with global properties of the loss surface. We define neural network Topological Obstructions score, TO-score, with help of robust topological invariants, barcodes of loss function, that quantify the badness of local minima for gradient-based optimization. We have made several experiments for computing these invariants, for small neural networks, and for fully connected, convolutional and ResNet-like neural networks on different datasets: MNIST, Fashion MNIST, CIFAR10, SVHN. Our two principal observations are as follows. Firstly, the neural network barcode and TO-score decrease with the increase of the neural network depth and width. Secondly, there is an intriguing connection between the length of minima segments in the barcode and the minima generalization error.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge