On the Performance of Gradient Tracking with Local Updates

We study the decentralized optimization problem where a network of $n$ agents seeks to minimize the average of a set of heterogeneous non-convex cost functions distributedly. State-of-the-art decentralized algorithms like Exact Diffusion~(ED) and Gradient Tracking~(GT) involve communicating every iteration. However, communication is expensive, resource intensive, and slow. In this work, we analyze a locally updated GT method (LU-GT), where agents perform local recursions before interacting with their neighbors. While local updates have been shown to reduce communication overhead in practice, their theoretical influence has not been fully characterized. We show LU-GT has the same communication complexity as the Federated Learning setting but allows arbitrary network topologies. In addition, we prove that the number of local updates does not degrade the quality of the solution achieved by LU-GT. Numerical examples reveal that local updates can lower communication costs in certain regimes (e.g., well-connected graphs).

On Acceleration of Gradient-Based Empirical Risk Minimization using Local Polynomial Regression

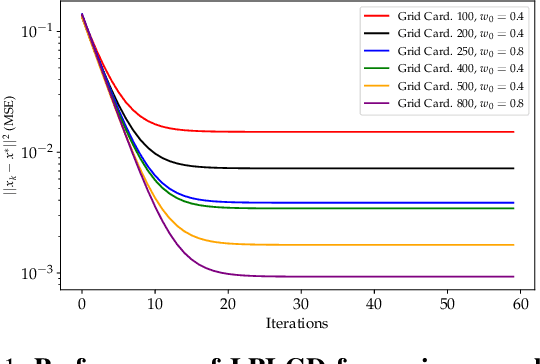
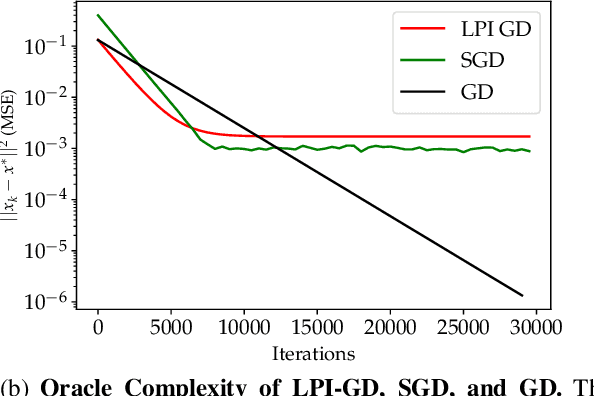
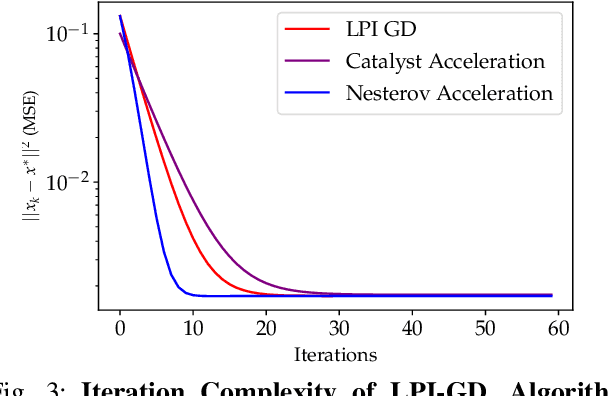
We study the acceleration of the Local Polynomial Interpolation-based Gradient Descent method (LPI-GD) recently proposed for the approximate solution of empirical risk minimization problems (ERM). We focus on loss functions that are strongly convex and smooth with condition number $\sigma$. We additionally assume the loss function is $\eta$-H\"older continuous with respect to the data. The oracle complexity of LPI-GD is $\tilde{O}\left(\sigma m^d \log(1/\varepsilon)\right)$ for a desired accuracy $\varepsilon$, where $d$ is the dimension of the parameter space, and $m$ is the cardinality of an approximation grid. The factor $m^d$ can be shown to scale as $O((1/\varepsilon)^{d/2\eta})$. LPI-GD has been shown to have better oracle complexity than gradient descent (GD) and stochastic gradient descent (SGD) for certain parameter regimes. We propose two accelerated methods for the ERM problem based on LPI-GD and show an oracle complexity of $\tilde{O}\left(\sqrt{\sigma} m^d \log(1/\varepsilon)\right)$. Moreover, we provide the first empirical study on local polynomial interpolation-based gradient methods and corroborate that LPI-GD has better performance than GD and SGD in some scenarios, and the proposed methods achieve acceleration.