Navigating Explanatory Multiverse Through Counterfactual Path Geometry

Counterfactual explanations are the de facto standard when tasked with interpreting decisions of (opaque) predictive models. Their generation is often subject to algorithmic and domain-specific constraints -- such as density-based feasibility for the former and attribute (im)mutability or directionality of change for the latter -- that aim to maximise their real-life utility. In addition to desiderata with respect to the counterfactual instance itself, the existence of a viable path connecting it with the factual data point, known as algorithmic recourse, has become an important technical consideration. While both of these requirements ensure that the steps of the journey as well as its destination are admissible, current literature neglects the multiplicity of such counterfactual paths. To address this shortcoming we introduce the novel concept of explanatory multiverse that encompasses all the possible counterfactual journeys and shows how to navigate, reason about and compare the geometry of these paths -- their affinity, branching, divergence and possible future convergence -- with two methods: vector spaces and graphs. Implementing this (interactive) explanatory process grants explainees more agency by allowing them to select counterfactuals based on the properties of the journey leading to them in addition to their absolute differences.

An Analysis of Physics-Informed Neural Networks

Whilst the partial differential equations that govern the dynamics of our world have been studied in great depth for centuries, solving them for complex, high-dimensional conditions and domains still presents an incredibly large mathematical and computational challenge. Analytical methods can be cumbersome to utilise, and numerical methods can lead to errors and inaccuracies. On top of this, sometimes we lack the information or knowledge to pose the problem well enough to apply these kinds of methods. Here, we present a new approach to approximating the solution to physical systems - physics-informed neural networks. The concept of artificial neural networks is introduced, the objective function is defined, and optimisation strategies are discussed. The partial differential equation is then included as a constraint in the loss function for the optimisation problem, giving the network access to knowledge of the dynamics of the physical system it is modelling. Some intuitive examples are displayed, and more complex applications are considered to showcase the power of physics informed neural networks, such as in seismic imaging. Solution error is analysed, and suggestions are made to improve convergence and/or solution precision. Problems and limitations are also touched upon in the conclusions, as well as some thoughts as to where physics informed neural networks are most useful, and where they could go next.

Helpful, Misleading or Confusing: How Humans Perceive Fundamental Building Blocks of Artificial Intelligence Explanations

Explainable artificial intelligence techniques are evolving at breakneck speed, but suitable evaluation approaches currently lag behind. With explainers becoming increasingly complex and a lack of consensus on how to assess their utility, it is challenging to judge the benefit and effectiveness of different explanations. To address this gap, we take a step back from complex predictive algorithms and instead look into explainability of simple mathematical models. In this setting, we aim to assess how people perceive comprehensibility of different model representations such as mathematical formulation, graphical representation and textual summarisation (of varying scope). This allows diverse stakeholders -- engineers, researchers, consumers, regulators and the like -- to judge intelligibility of fundamental concepts that more complex artificial intelligence explanations are built from. This position paper charts our approach to establishing appropriate evaluation methodology as well as a conceptual and practical framework to facilitate setting up and executing relevant user studies.

How Robust is your Fair Model? Exploring the Robustness of Diverse Fairness Strategies

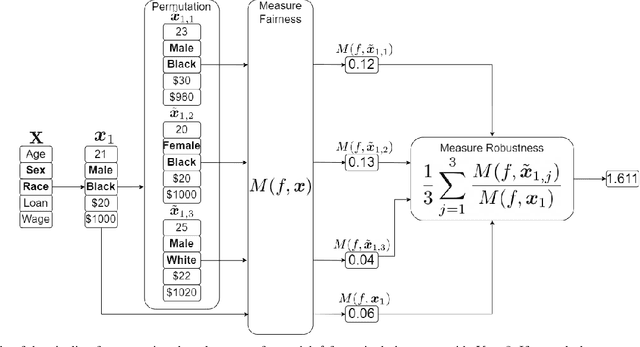
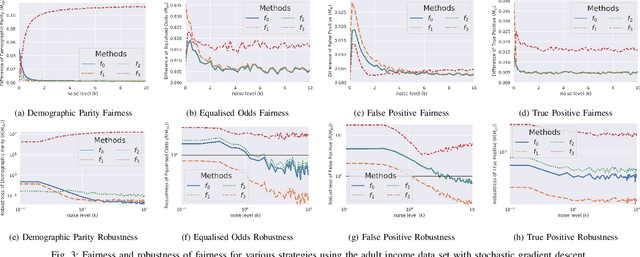
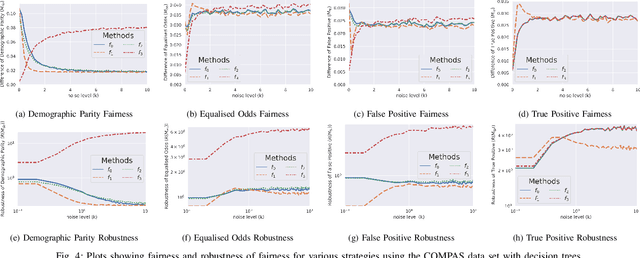
With the introduction of machine learning in high-stakes decision making, ensuring algorithmic fairness has become an increasingly important problem to solve. In response to this, many mathematical definitions of fairness have been proposed, and a variety of optimisation techniques have been developed, all designed to maximise a defined notion of fairness. However, fair solutions are reliant on the quality of the training data, and can be highly sensitive to noise. Recent studies have shown that robustness (the ability for a model to perform well on unseen data) plays a significant role in the type of strategy that should be used when approaching a new problem and, hence, measuring the robustness of these strategies has become a fundamental problem. In this work, we therefore propose a new criterion to measure the robustness of various fairness optimisation strategies - the robustness ratio. We conduct multiple extensive experiments on five bench mark fairness data sets using three of the most popular fairness strategies with respect to four of the most popular definitions of fairness. Our experiments empirically show that fairness methods that rely on threshold optimisation are very sensitive to noise in all the evaluated data sets, despite mostly outperforming other methods. This is in contrast to the other two methods, which are less fair for low noise scenarios but fairer for high noise ones. To the best of our knowledge, we are the first to quantitatively evaluate the robustness of fairness optimisation strategies. This can potentially can serve as a guideline in choosing the most suitable fairness strategy for various data sets.