Solving Novel Program Synthesis Problems with Genetic Programming using Parametric Polymorphism

Contemporary genetic programming (GP) systems for general program synthesis have been primarily concerned with evolving programs that can manipulate values from a standard set of primitive data types and simple indexed data structures. In contrast, human programmers do not limit themselves to a small finite set of data types and use polymorphism to express an unbounded number of types including nested data structures, product types, and generic functions. Code-building Genetic Programming (CBGP) is a recently introduced method that compiles type-safe programs from linear genomes using stack-based compilation and a formal type system. Although prior work with CBGP has shown initial demonstrations of polymorphism inside evolved programs, we have provided a deeper exploration of these capabilities through the evolution of programs which make use of generic data types such as key-value maps, tuples, and sets, as well as higher order functions and functions with polymorphic type signatures. In our experiments, CBGP is able to solve problems with all of these properties, where every other GP system that we know of has restrictions that make it unable to even consider problems with these properties. This demonstration provides a significant step towards fully aligning the expressiveness of GP to real world programming.

Probabilistic Lexicase Selection

Lexicase selection is a widely used parent selection algorithm in genetic programming, known for its success in various task domains such as program synthesis, symbolic regression, and machine learning. Due to its non-parametric and recursive nature, calculating the probability of each individual being selected by lexicase selection has been proven to be an NP-hard problem, which discourages deeper theoretical understanding and practical improvements to the algorithm. In this work, we introduce probabilistic lexicase selection (plexicase selection), a novel parent selection algorithm that efficiently approximates the probability distribution of lexicase selection. Our method not only demonstrates superior problem-solving capabilities as a semantic-aware selection method, but also benefits from having a probabilistic representation of the selection process for enhanced efficiency and flexibility. Experiments are conducted in two prevalent domains in genetic programming: program synthesis and symbolic regression, using standard benchmarks including PSB and SRBench. The empirical results show that plexicase selection achieves state-of-the-art problem-solving performance that is competitive to the lexicase selection, and significantly outperforms lexicase selection in computation efficiency.

Functional Code Building Genetic Programming

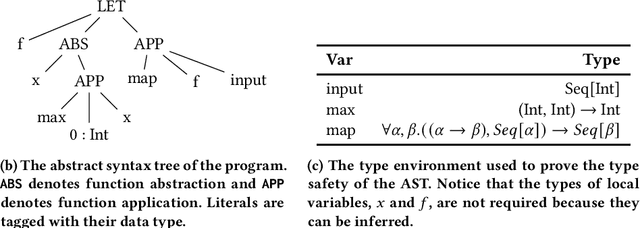
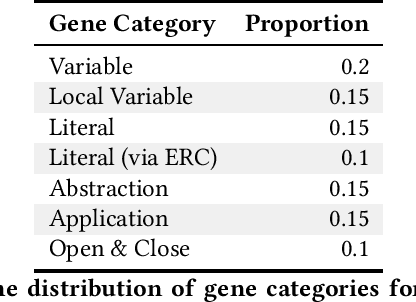
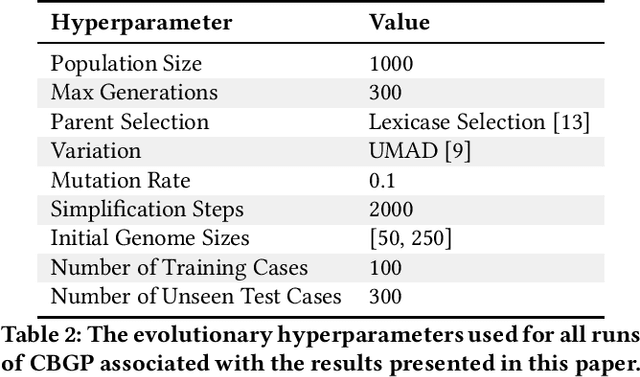
General program synthesis has become an important application area for genetic programming (GP), and for artificial intelligence more generally. Code Building Genetic Programming (CBGP) is a recently introduced GP method for general program synthesis that leverages reflection and first class specifications to support the evolution of programs that may use arbitrary data types, polymorphism, and functions drawn from existing codebases. However, neither a formal description nor a thorough benchmarking of CBGP have yet been reported. In this work, we formalize the method of CBGP using algorithms from type theory. Specially, we show that a functional programming language and a Hindley-Milner type system can be used to evolve type-safe programs using the process abstractly described in the original CBGP paper. Furthermore, we perform a comprehensive analysis of the search performance of this functional variant of CBGP compared to other contemporary GP program synthesis methods.

Independence Tests Without Ground Truth for Noisy Learners

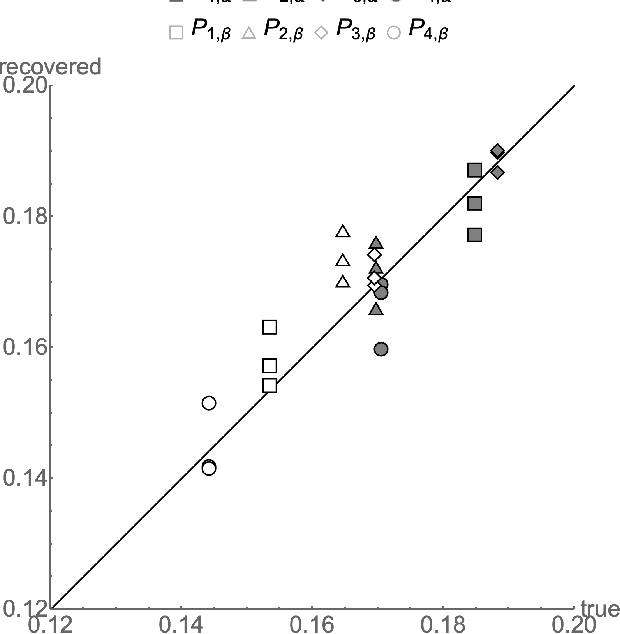
Exact ground truth invariant polynomial systems can be written for arbitrarily correlated binary classifiers. Their solutions give estimates for sample statistics that require knowledge of the ground truth of the correct labels in the sample. Of these polynomial systems, only a few have been solved in closed form. Here we discuss the exact solution for independent binary classifiers - resolving an outstanding problem that has been presented at this conference and others. Its practical applicability is hampered by its sole remaining assumption - the classifiers need to be independent in their sample errors. We discuss how to use the closed form solution to create a self-consistent test that can validate the independence assumption itself absent the correct labels ground truth. It can be cast as an algebraic geometry conjecture for binary classifiers that remains unsolved. A similar conjecture for the ground truth invariant algebraic system for scalar regressors is solvable, and we present the solution here. We also discuss experiments on the Penn ML Benchmark classification tasks that provide further evidence that the conjecture may be true for the polynomial system of binary classifiers.

Code Building Genetic Programming

In recent years the field of genetic programming has made significant advances towards automatic programming. Research and development of contemporary program synthesis methods, such as PushGP and Grammar Guided Genetic Programming, can produce programs that solve problems typically assigned in introductory academic settings. These problems focus on a narrow, predetermined set of simple data structures, basic control flow patterns, and primitive, non-overlapping data types (without, for example, inheritance or composite types). Few, if any, genetic programming methods for program synthesis have convincingly demonstrated the capability of synthesizing programs that use arbitrary data types, data structures, and specifications that are drawn from existing codebases. In this paper, we introduce Code Building Genetic Programming (CBGP) as a framework within which this can be done, by leveraging programming language features such as reflection and first-class specifications. CBGP produces a computational graph that can be executed or translated into source code of a host language. To demonstrate the novel capabilities of CBGP, we present results on new benchmarks that use non-primitive, polymorphic data types as well as some standard program synthesis benchmarks.

Algebraic Ground Truth Inference: Non-Parametric Estimation of Sample Errors by AI Algorithms

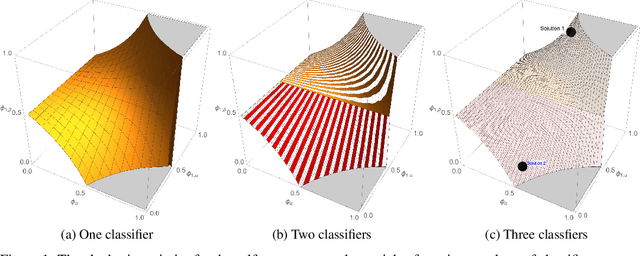
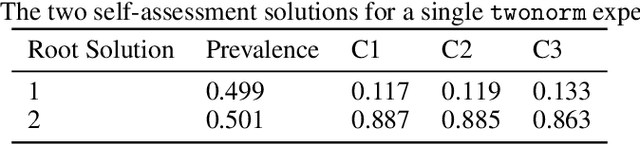
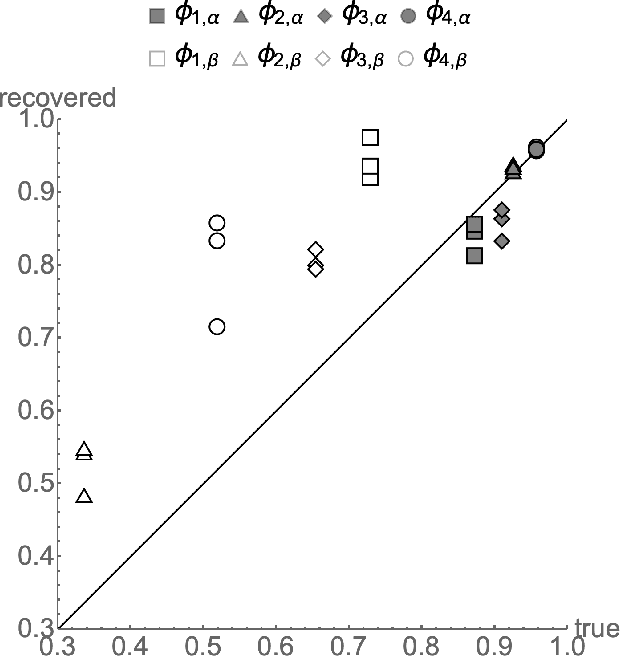
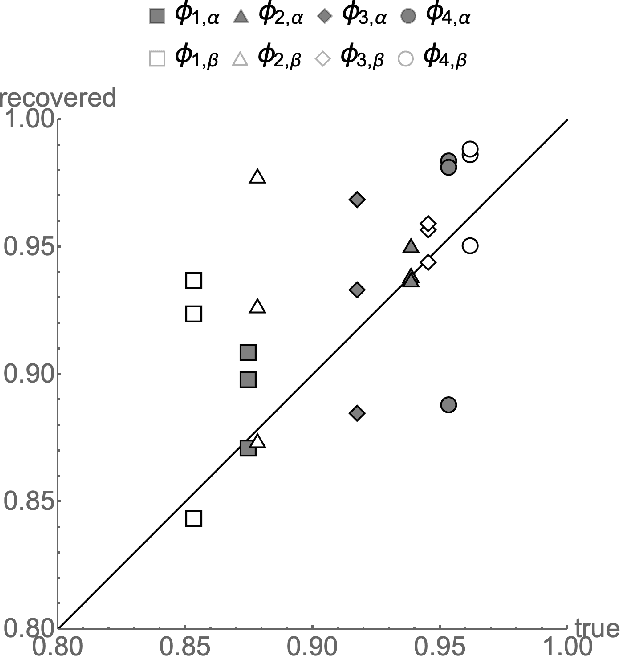
Binary classification is widely used in ML production systems. Monitoring classifiers in a constrained event space is well known. However, real world production systems often lack the ground truth these methods require. Privacy concerns may also require that the ground truth needed to evaluate the classifiers cannot be made available. In these autonomous settings, non-parametric estimators of performance are an attractive solution. They do not require theoretical models about how the classifiers made errors in any given sample. They just estimate how many errors there are in a sample of an industrial or robotic datastream. We construct one such non-parametric estimator of the sample errors for an ensemble of weak binary classifiers. Our approach uses algebraic geometry to reformulate the self-assessment problem for ensembles of binary classifiers as an exact polynomial system. The polynomial formulation can then be used to prove - as an algebraic geometry algorithm - that no general solution to the self-assessment problem is possible. However, specific solutions are possible in settings where the engineering context puts the classifiers close to independent errors. The practical utility of the method is illustrated on a real-world dataset from an online advertising campaign and a sample of common classification benchmarks. The accuracy estimators in the experiments where we have ground truth are better than one part in a hundred. The online advertising campaign data, where we do not have ground truth data, is verified by an internal consistency approach whose validity we conjecture as an algebraic geometry theorem. We call this approach - algebraic ground truth inference.

Error Correcting Algorithms for Sparsely Correlated Regressors

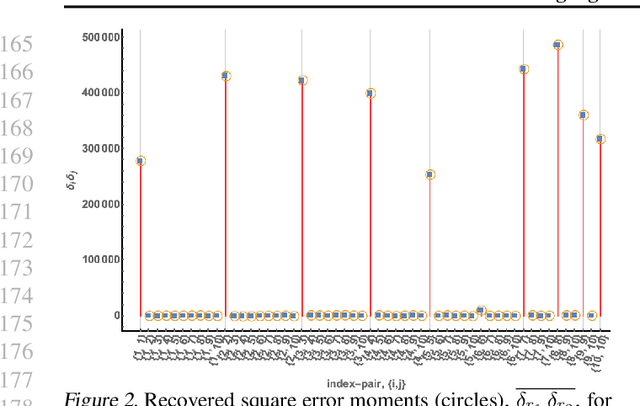
Autonomy and adaptation of machines requires that they be able to measure their own errors. We consider the advantages and limitations of such an approach when a machine has to measure the error in a regression task. How can a machine measure the error of regression sub-components when it does not have the ground truth for the correct predictions? A compressed sensing approach applied to the error signal of the regressors can recover their precision error without any ground truth. It allows for some regressors to be \emph{strongly correlated} as long as not too many are so related. Its solutions, however, are not unique - a property of ground truth inference solutions. Adding $\ell_1$--minimization as a condition can recover the correct solution in settings where error correction is possible. We briefly discuss the similarity of the mathematics of ground truth inference for regressors to that for classifiers.

Lexicase Selection of Specialists

Lexicase parent selection filters the population by considering one random training case at a time, eliminating any individuals with errors for the current case that are worse than the best error in the selection pool, until a single individual remains. This process often stops before considering all training cases, meaning that it will ignore the error values on any cases that were not yet considered. Lexicase selection can therefore select specialist individuals that have poor errors on some training cases, if they have great errors on others and those errors come near the start of the random list of cases used for the parent selection event in question. We hypothesize here that selecting these specialists, which may have poor total error, plays an important role in lexicase selection's observed performance advantages over error-aggregating parent selection methods such as tournament selection, which select specialists much less frequently. We conduct experiments examining this hypothesis, and find that lexicase selection's performance and diversity maintenance degrade when we deprive it of the ability of selecting specialists. These findings help explain the improved performance of lexicase selection compared to tournament selection, and suggest that specialists help drive evolution under lexicase selection toward global solutions.