Eddie Zahrebelski
Independence Tests Without Ground Truth for Noisy Learners
Oct 28, 2020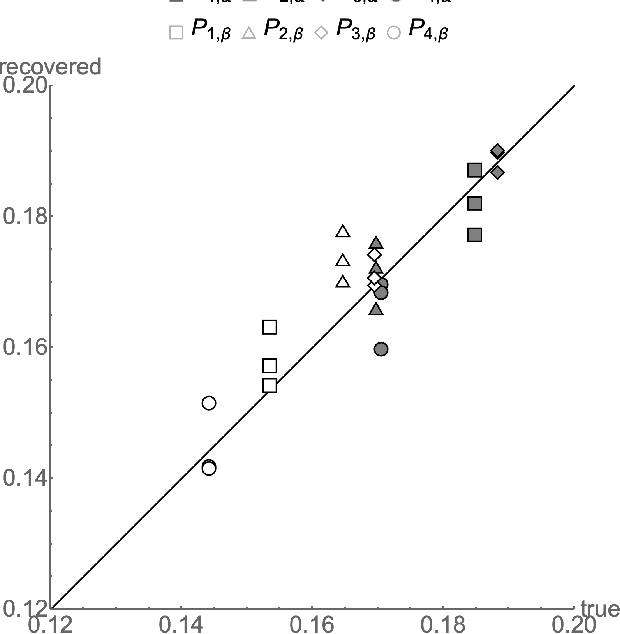
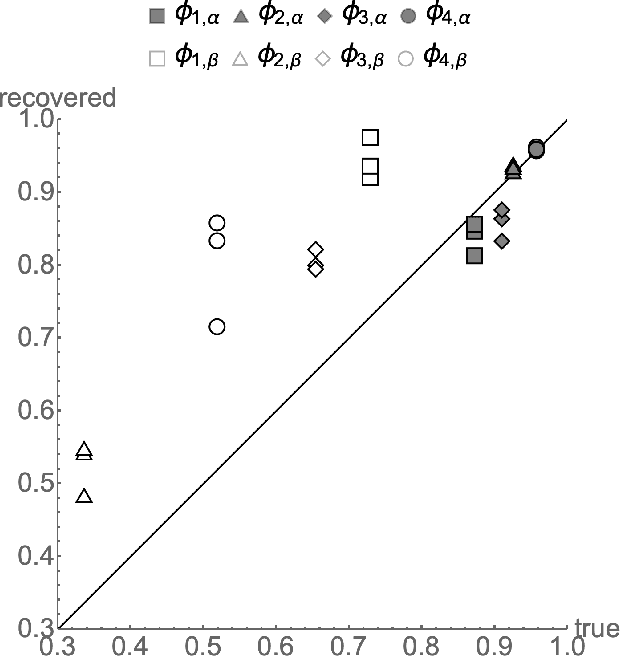
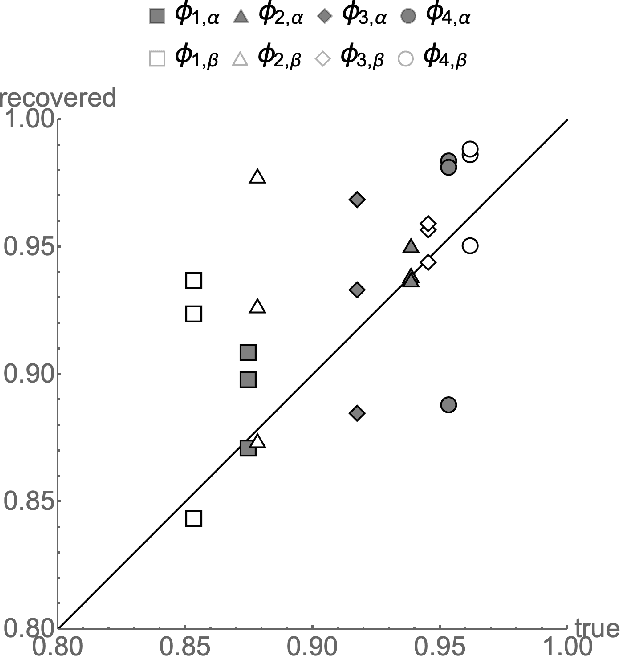

Abstract:Exact ground truth invariant polynomial systems can be written for arbitrarily correlated binary classifiers. Their solutions give estimates for sample statistics that require knowledge of the ground truth of the correct labels in the sample. Of these polynomial systems, only a few have been solved in closed form. Here we discuss the exact solution for independent binary classifiers - resolving an outstanding problem that has been presented at this conference and others. Its practical applicability is hampered by its sole remaining assumption - the classifiers need to be independent in their sample errors. We discuss how to use the closed form solution to create a self-consistent test that can validate the independence assumption itself absent the correct labels ground truth. It can be cast as an algebraic geometry conjecture for binary classifiers that remains unsolved. A similar conjecture for the ground truth invariant algebraic system for scalar regressors is solvable, and we present the solution here. We also discuss experiments on the Penn ML Benchmark classification tasks that provide further evidence that the conjecture may be true for the polynomial system of binary classifiers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge