Aditya Chaganti
Independence Tests Without Ground Truth for Noisy Learners
Oct 28, 2020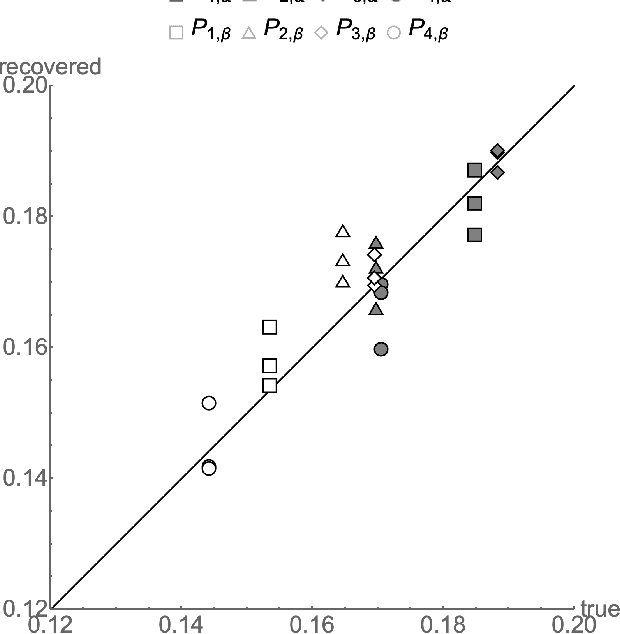

Abstract:Exact ground truth invariant polynomial systems can be written for arbitrarily correlated binary classifiers. Their solutions give estimates for sample statistics that require knowledge of the ground truth of the correct labels in the sample. Of these polynomial systems, only a few have been solved in closed form. Here we discuss the exact solution for independent binary classifiers - resolving an outstanding problem that has been presented at this conference and others. Its practical applicability is hampered by its sole remaining assumption - the classifiers need to be independent in their sample errors. We discuss how to use the closed form solution to create a self-consistent test that can validate the independence assumption itself absent the correct labels ground truth. It can be cast as an algebraic geometry conjecture for binary classifiers that remains unsolved. A similar conjecture for the ground truth invariant algebraic system for scalar regressors is solvable, and we present the solution here. We also discuss experiments on the Penn ML Benchmark classification tasks that provide further evidence that the conjecture may be true for the polynomial system of binary classifiers.
Algebraic Ground Truth Inference: Non-Parametric Estimation of Sample Errors by AI Algorithms
Jun 15, 2020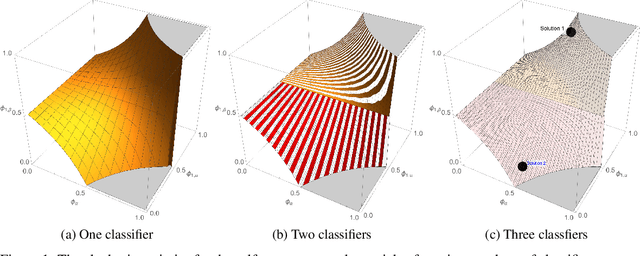

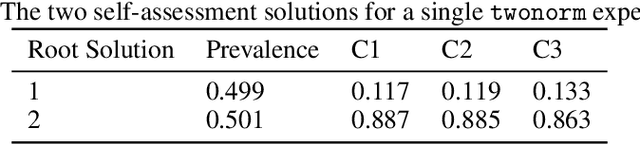

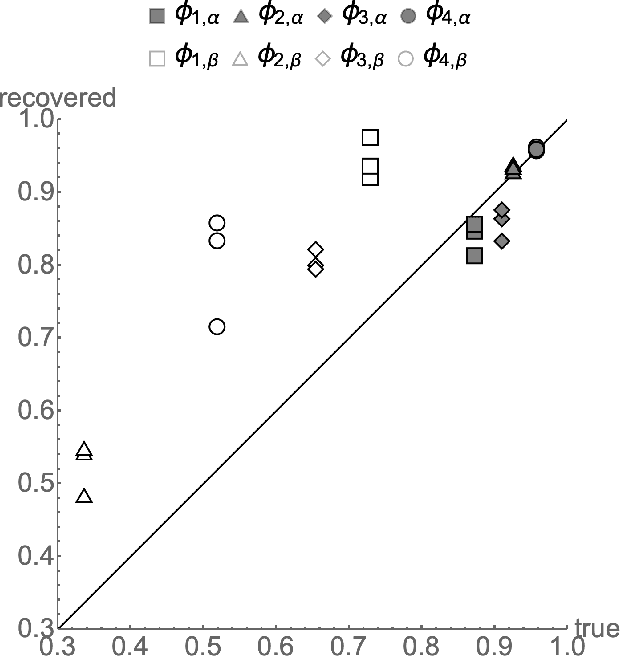
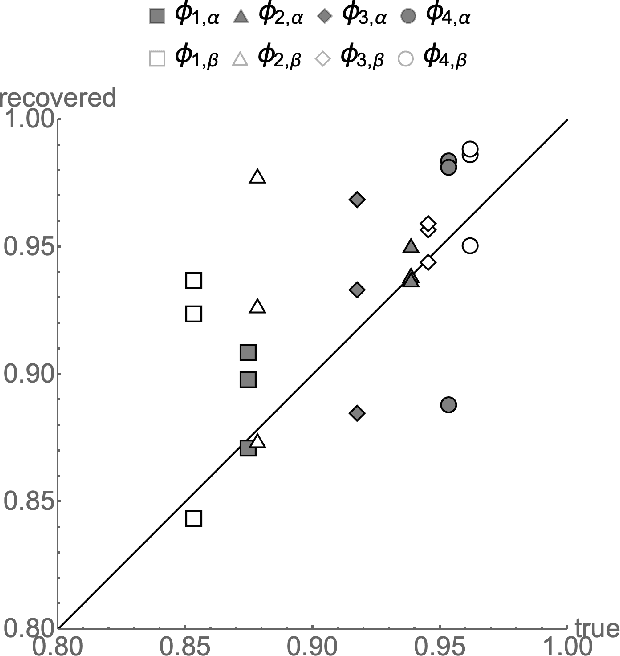
Abstract:Binary classification is widely used in ML production systems. Monitoring classifiers in a constrained event space is well known. However, real world production systems often lack the ground truth these methods require. Privacy concerns may also require that the ground truth needed to evaluate the classifiers cannot be made available. In these autonomous settings, non-parametric estimators of performance are an attractive solution. They do not require theoretical models about how the classifiers made errors in any given sample. They just estimate how many errors there are in a sample of an industrial or robotic datastream. We construct one such non-parametric estimator of the sample errors for an ensemble of weak binary classifiers. Our approach uses algebraic geometry to reformulate the self-assessment problem for ensembles of binary classifiers as an exact polynomial system. The polynomial formulation can then be used to prove - as an algebraic geometry algorithm - that no general solution to the self-assessment problem is possible. However, specific solutions are possible in settings where the engineering context puts the classifiers close to independent errors. The practical utility of the method is illustrated on a real-world dataset from an online advertising campaign and a sample of common classification benchmarks. The accuracy estimators in the experiments where we have ground truth are better than one part in a hundred. The online advertising campaign data, where we do not have ground truth data, is verified by an internal consistency approach whose validity we conjecture as an algebraic geometry theorem. We call this approach - algebraic ground truth inference.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge