A logical alarm for misaligned binary classifiers

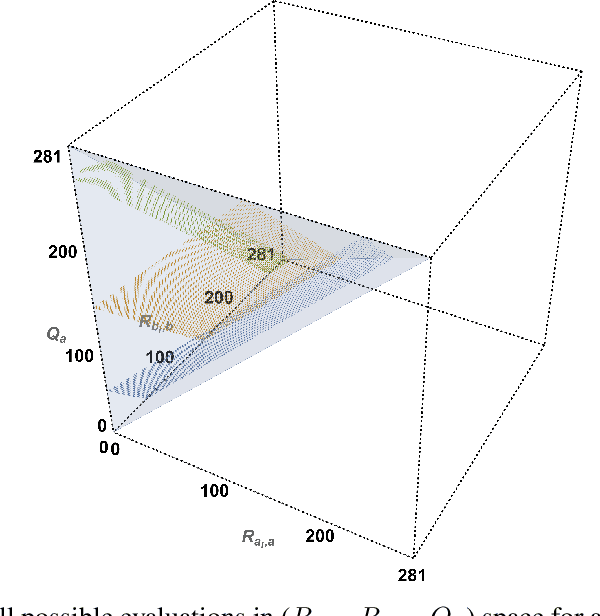
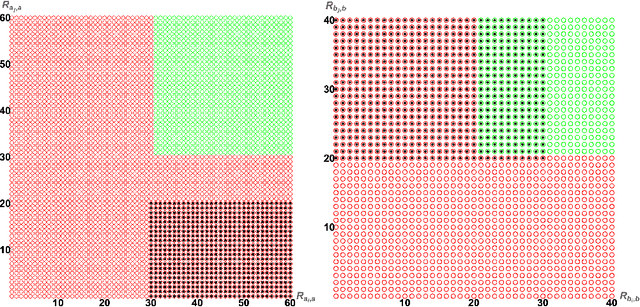
If two agents disagree in their decisions, we may suspect they are not both correct. This intuition is formalized for evaluating agents that have carried out a binary classification task. Their agreements and disagreements on a joint test allow us to establish the only group evaluations logically consistent with their responses. This is done by establishing a set of axioms (algebraic relations) that must be universally obeyed by all evaluations of binary responders. A complete set of such axioms are possible for each ensemble of size N. The axioms for $N = 1, 2$ are used to construct a fully logical alarm - one that can prove that at least one ensemble member is malfunctioning using only unlabeled data. The similarities of this approach to formal software verification and its utility for recent agendas of safe guaranteed AI are discussed.

The logic of NTQR evaluations of noisy AI agents: Complete postulates and logically consistent error correlations

In his "ship of state" allegory (\textit{Republic}, Book VI, 488) Plato poses a question -- how can a crew of sailors presumed to know little about the art of navigation recognize the true pilot among them? The allegory argues that a simple majority voting procedure cannot safely determine who is most qualified to pilot a ship when the voting members are ignorant or biased. We formalize Plato's concerns by considering the problem in AI safety of monitoring noisy AI agents in unsupervised settings. An algorithm evaluating AI agents using unlabeled data would be subject to the evaluation dilemma - how would we know the evaluation algorithm was correct itself? This endless validation chain can be avoided by considering purely algebraic functions of the observed responses. We can construct complete postulates than can prove or disprove the logical consistency of any grading algorithm. A complete set of postulates exists whenever we are evaluating $N$ experts that took $T$ tests with $Q$ questions with $R$ responses each. We discuss evaluating binary classifiers that have taken a single test - the $(N,T=1,Q,R=2)$ tests. We show how some of the postulates have been previously identified in the ML literature but not recognized as such - the \textbf{agreement equations} of Platanios. The complete postulates for pair correlated binary classifiers are considered and we show how it allows for error correlations to be quickly calculated. An algebraic evaluator based on the assumption that the ensemble is error independent is compared with grading by majority voting on evaluations using the \uciadult and and \texttt{two-norm} datasets. Throughout, we demonstrate how the formalism of logical consistency via algebraic postulates of evaluation can help increase the safety of machines using AI algorithms.

Streaming algorithms for evaluating noisy judges on unlabeled data -- binary classification

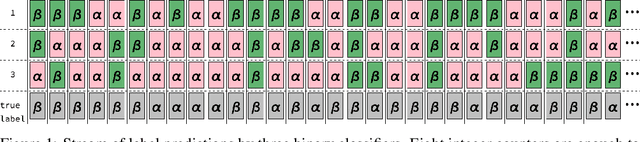
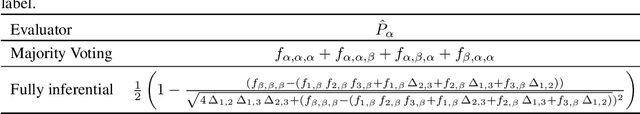
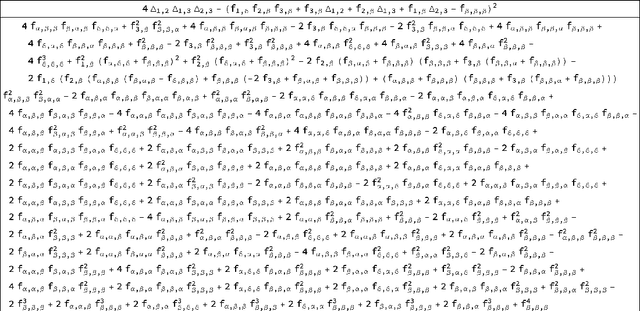
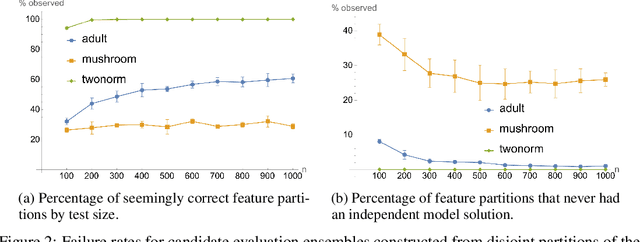
The evaluation of noisy binary classifiers on unlabeled data is treated as a streaming task: given a data sketch of the decisions by an ensemble, estimate the true prevalence of the labels as well as each classifier's accuracy on them. Two fully algebraic evaluators are constructed to do this. Both are based on the assumption that the classifiers make independent errors. The first is based on majority voting. The second, the main contribution of the paper, is guaranteed to be correct. But how do we know the classifiers are independent on any given test? This principal/agent monitoring paradox is ameliorated by exploiting the failures of the independent evaluator to return sensible estimates. A search for nearly error independent trios is empirically carried out on the \texttt{adult}, \texttt{mushroom}, and \texttt{two-norm} datasets by using the algebraic failure modes to reject evaluation ensembles as too correlated. The searches are refined by constructing a surface in evaluation space that contains the true value point. The algebra of arbitrarily correlated classifiers permits the selection of a polynomial subset free of any correlation variables. Candidate evaluation ensembles are rejected if their data sketches produce independent estimates too far from the constructed surface. The results produced by the surviving ensembles can sometimes be as good as 1\%. But handling even small amounts of correlation remains a challenge. A Taylor expansion of the estimates produced when independence is assumed but the classifiers are, in fact, slightly correlated helps clarify how the independent evaluator has algebraic `blind spots'.

Independence Tests Without Ground Truth for Noisy Learners

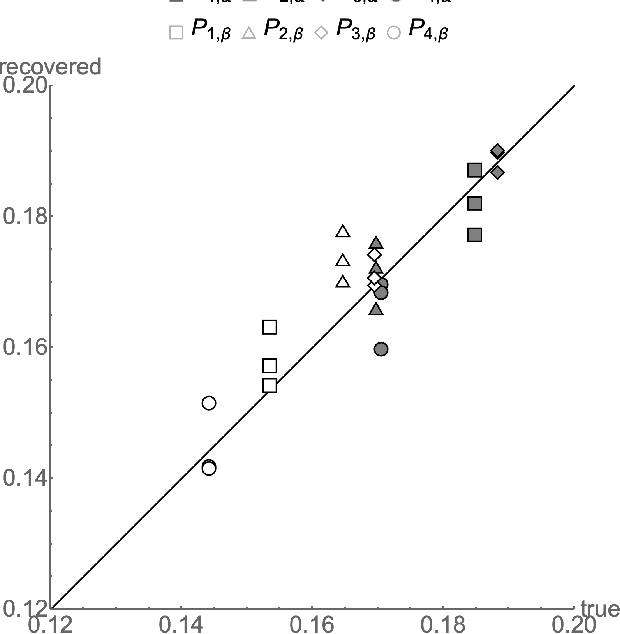
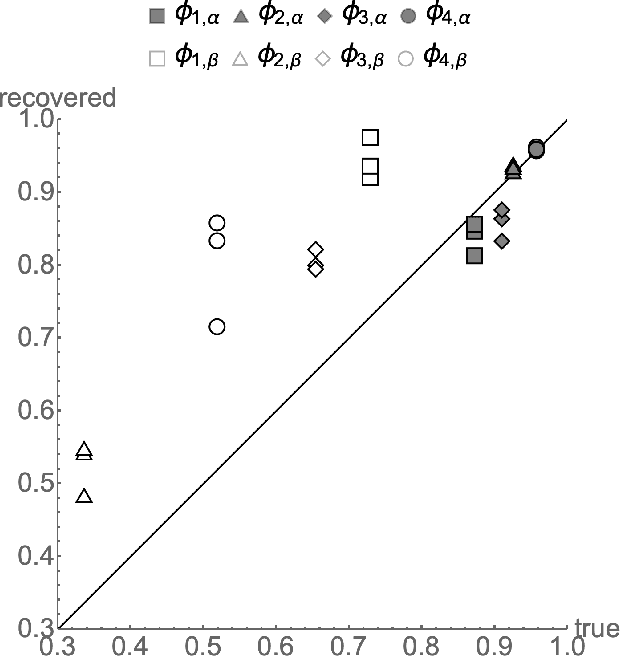
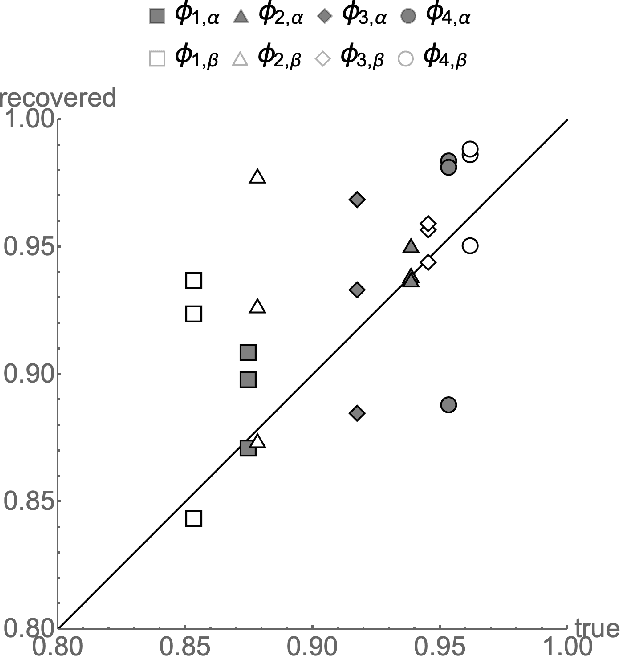
Exact ground truth invariant polynomial systems can be written for arbitrarily correlated binary classifiers. Their solutions give estimates for sample statistics that require knowledge of the ground truth of the correct labels in the sample. Of these polynomial systems, only a few have been solved in closed form. Here we discuss the exact solution for independent binary classifiers - resolving an outstanding problem that has been presented at this conference and others. Its practical applicability is hampered by its sole remaining assumption - the classifiers need to be independent in their sample errors. We discuss how to use the closed form solution to create a self-consistent test that can validate the independence assumption itself absent the correct labels ground truth. It can be cast as an algebraic geometry conjecture for binary classifiers that remains unsolved. A similar conjecture for the ground truth invariant algebraic system for scalar regressors is solvable, and we present the solution here. We also discuss experiments on the Penn ML Benchmark classification tasks that provide further evidence that the conjecture may be true for the polynomial system of binary classifiers.

Algebraic Ground Truth Inference: Non-Parametric Estimation of Sample Errors by AI Algorithms

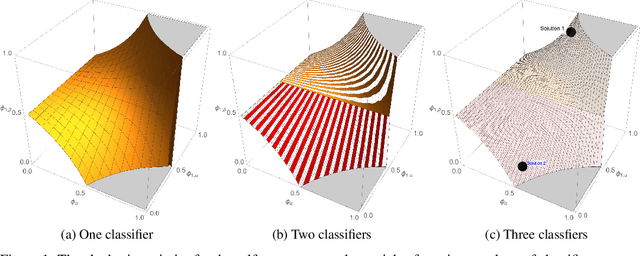
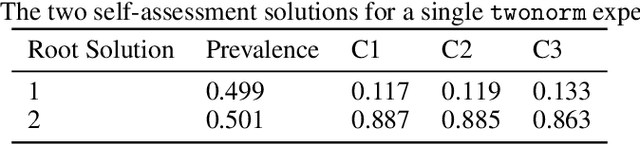
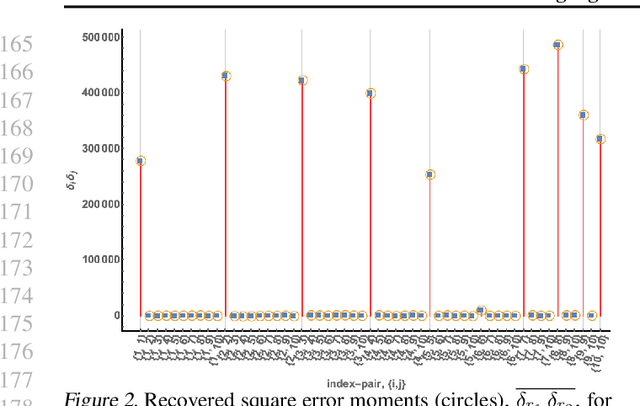
Binary classification is widely used in ML production systems. Monitoring classifiers in a constrained event space is well known. However, real world production systems often lack the ground truth these methods require. Privacy concerns may also require that the ground truth needed to evaluate the classifiers cannot be made available. In these autonomous settings, non-parametric estimators of performance are an attractive solution. They do not require theoretical models about how the classifiers made errors in any given sample. They just estimate how many errors there are in a sample of an industrial or robotic datastream. We construct one such non-parametric estimator of the sample errors for an ensemble of weak binary classifiers. Our approach uses algebraic geometry to reformulate the self-assessment problem for ensembles of binary classifiers as an exact polynomial system. The polynomial formulation can then be used to prove - as an algebraic geometry algorithm - that no general solution to the self-assessment problem is possible. However, specific solutions are possible in settings where the engineering context puts the classifiers close to independent errors. The practical utility of the method is illustrated on a real-world dataset from an online advertising campaign and a sample of common classification benchmarks. The accuracy estimators in the experiments where we have ground truth are better than one part in a hundred. The online advertising campaign data, where we do not have ground truth data, is verified by an internal consistency approach whose validity we conjecture as an algebraic geometry theorem. We call this approach - algebraic ground truth inference.

Error Correcting Algorithms for Sparsely Correlated Regressors

Autonomy and adaptation of machines requires that they be able to measure their own errors. We consider the advantages and limitations of such an approach when a machine has to measure the error in a regression task. How can a machine measure the error of regression sub-components when it does not have the ground truth for the correct predictions? A compressed sensing approach applied to the error signal of the regressors can recover their precision error without any ground truth. It allows for some regressors to be \emph{strongly correlated} as long as not too many are so related. Its solutions, however, are not unique - a property of ground truth inference solutions. Adding $\ell_1$--minimization as a condition can recover the correct solution in settings where error correction is possible. We briefly discuss the similarity of the mathematics of ground truth inference for regressors to that for classifiers.