Sub-Goal Trees -- a Framework for Goal-Based Reinforcement Learning

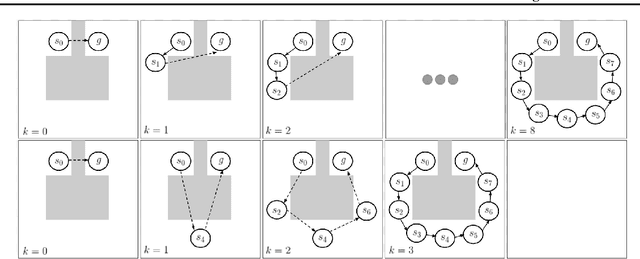
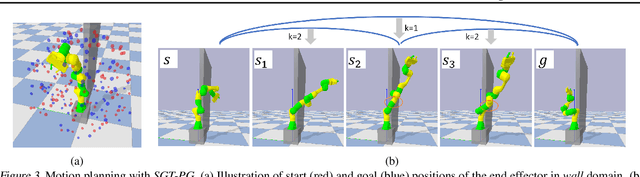
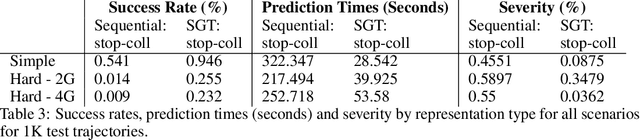
Many AI problems, in robotics and other domains, are goal-based, essentially seeking trajectories leading to various goal states. Reinforcement learning (RL), building on Bellman's optimality equation, naturally optimizes for a single goal, yet can be made multi-goal by augmenting the state with the goal. Instead, we propose a new RL framework, derived from a dynamic programming equation for the all pairs shortest path (APSP) problem, which naturally solves multi-goal queries. We show that this approach has computational benefits for both standard and approximate dynamic programming. Interestingly, our formulation prescribes a novel protocol for computing a trajectory: instead of predicting the next state given its predecessor, as in standard RL, a goal-conditioned trajectory is constructed by first predicting an intermediate state between start and goal, partitioning the trajectory into two. Then, recursively, predicting intermediate points on each sub-segment, until a complete trajectory is obtained. We call this trajectory structure a sub-goal tree. Building on it, we additionally extend the policy gradient methodology to recursively predict sub-goals, resulting in novel goal-based algorithms. Finally, we apply our method to neural motion planning, where we demonstrate significant improvements compared to standard RL on navigating a 7-DoF robot arm between obstacles.

Sub-Goal Trees -- a Framework for Goal-Directed Trajectory Prediction and Optimization

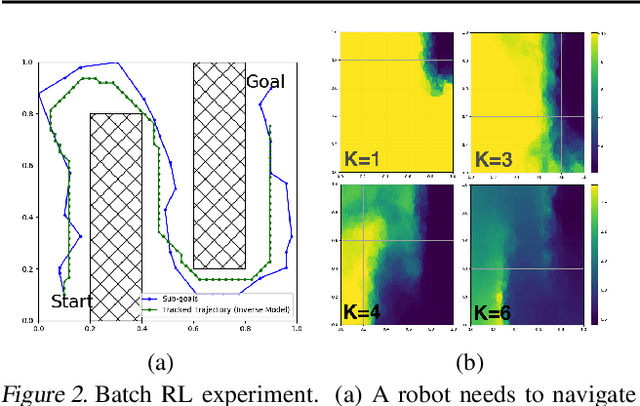
Many AI problems, in robotics and other domains, are goal-directed, essentially seeking a trajectory leading to some goal state. In such problems, the way we choose to represent a trajectory underlies algorithms for trajectory prediction and optimization. Interestingly, most all prior work in imitation and reinforcement learning builds on a sequential trajectory representation -- calculating the next state in the trajectory given its predecessors. We propose a different perspective: a goal-conditioned trajectory can be represented by first selecting an intermediate state between start and goal, partitioning the trajectory into two. Then, recursively, predicting intermediate points on each sub-segment, until a complete trajectory is obtained. We call this representation a sub-goal tree, and building on it, we develop new methods for trajectory prediction, learning, and optimization. We show that in a supervised learning setting, sub-goal trees better account for trajectory variability, and can predict trajectories exponentially faster at test time by leveraging a concurrent computation. Then, for optimization, we derive a new dynamic programming equation for sub-goal trees, and use it to develop new planning and reinforcement learning algorithms. These algorithms, which are not based on the standard Bellman equation, naturally account for hierarchical sub-goal structure in a task. Empirical results on motion planning domains show that the sub-goal tree framework significantly improves both accuracy and prediction time.

Learning Generalized Reactive Policies using Deep Neural Networks

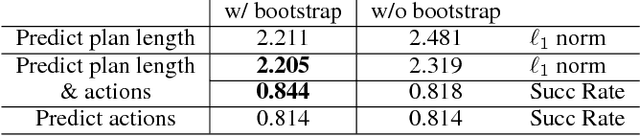
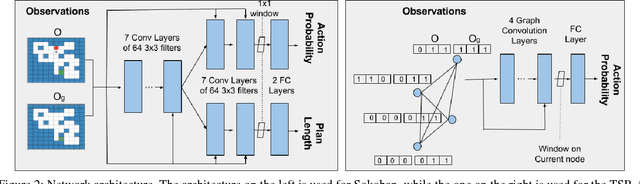
We present a new approach to learning for planning, where knowledge acquired while solving a given set of planning problems is used to plan faster in related, but new problem instances. We show that a deep neural network can be used to learn and represent a \emph{generalized reactive policy} (GRP) that maps a problem instance and a state to an action, and that the learned GRPs efficiently solve large classes of challenging problem instances. In contrast to prior efforts in this direction, our approach significantly reduces the dependence of learning on handcrafted domain knowledge or feature selection. Instead, the GRP is trained from scratch using a set of successful execution traces. We show that our approach can also be used to automatically learn a heuristic function that can be used in directed search algorithms. We evaluate our approach using an extensive suite of experiments on two challenging planning problem domains and show that our approach facilitates learning complex decision making policies and powerful heuristic functions with minimal human input. Videos of our results are available at goo.gl/Hpy4e3.