Learning Generalized Reactive Policies using Deep Neural Networks

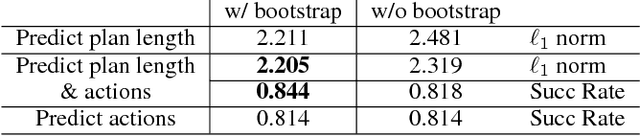
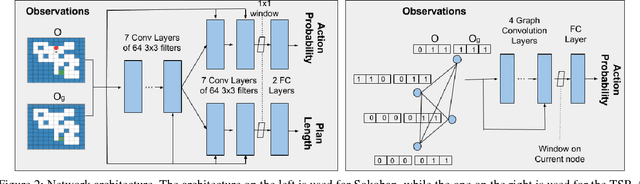
We present a new approach to learning for planning, where knowledge acquired while solving a given set of planning problems is used to plan faster in related, but new problem instances. We show that a deep neural network can be used to learn and represent a \emph{generalized reactive policy} (GRP) that maps a problem instance and a state to an action, and that the learned GRPs efficiently solve large classes of challenging problem instances. In contrast to prior efforts in this direction, our approach significantly reduces the dependence of learning on handcrafted domain knowledge or feature selection. Instead, the GRP is trained from scratch using a set of successful execution traces. We show that our approach can also be used to automatically learn a heuristic function that can be used in directed search algorithms. We evaluate our approach using an extensive suite of experiments on two challenging planning problem domains and show that our approach facilitates learning complex decision making policies and powerful heuristic functions with minimal human input. Videos of our results are available at goo.gl/Hpy4e3.

PAC-Bayes Control: Synthesizing Controllers that Provably Generalize to Novel Environments

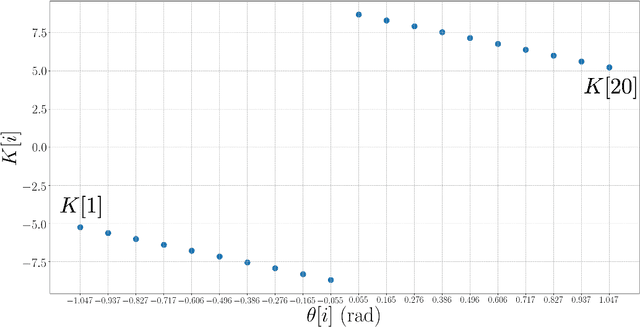
Our goal is to synthesize controllers for robots that provably generalize well to novel environments given a dataset of example environments. The key technical idea behind our approach is to leverage tools from generalization theory in machine learning by exploiting a precise analogy (which we present in the form of a reduction) between robustness of controllers to novel environments and generalization of hypotheses in supervised learning. In particular, we utilize the Probably Approximately Correct (PAC)-Bayes framework, which allows us to obtain upper bounds (that hold with high probability) on the expected cost of (stochastic) controllers across novel environments. We propose control synthesis algorithms that explicitly seek to minimize this upper bound. The corresponding optimization problem can be solved using convex optimization (Relative Entropy Programming in particular) in the setting where we are optimizing over a finite control policy space. In the more general setting of continuously parameterized controllers, we minimize this upper bound using stochastic gradient descent. We present examples of our approach in the context of obstacle avoidance control with depth measurements. Our simulated examples demonstrate the potential of our approach to provide strong generalization guarantees on controllers for robotic systems with continuous state and action spaces, complicated (e.g., nonlinear) dynamics, and rich sensory inputs (e.g., depth measurements).