Sub-Goal Trees -- a Framework for Goal-Directed Trajectory Prediction and Optimization
Paper and Code
Jun 12, 2019


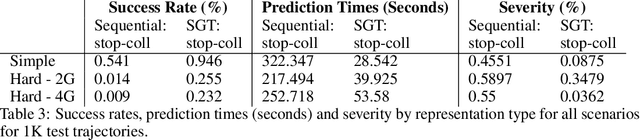
Many AI problems, in robotics and other domains, are goal-directed, essentially seeking a trajectory leading to some goal state. In such problems, the way we choose to represent a trajectory underlies algorithms for trajectory prediction and optimization. Interestingly, most all prior work in imitation and reinforcement learning builds on a sequential trajectory representation -- calculating the next state in the trajectory given its predecessors. We propose a different perspective: a goal-conditioned trajectory can be represented by first selecting an intermediate state between start and goal, partitioning the trajectory into two. Then, recursively, predicting intermediate points on each sub-segment, until a complete trajectory is obtained. We call this representation a sub-goal tree, and building on it, we develop new methods for trajectory prediction, learning, and optimization. We show that in a supervised learning setting, sub-goal trees better account for trajectory variability, and can predict trajectories exponentially faster at test time by leveraging a concurrent computation. Then, for optimization, we derive a new dynamic programming equation for sub-goal trees, and use it to develop new planning and reinforcement learning algorithms. These algorithms, which are not based on the standard Bellman equation, naturally account for hierarchical sub-goal structure in a task. Empirical results on motion planning domains show that the sub-goal tree framework significantly improves both accuracy and prediction time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge