Sub-Goal Trees -- a Framework for Goal-Based Reinforcement Learning
Paper and Code
Feb 27, 2020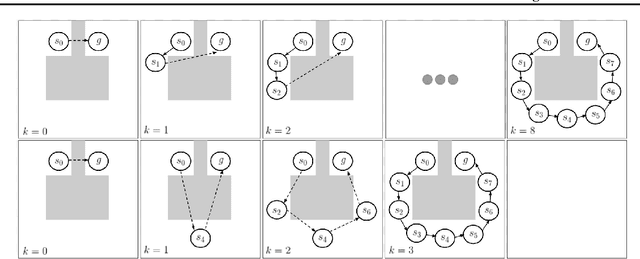
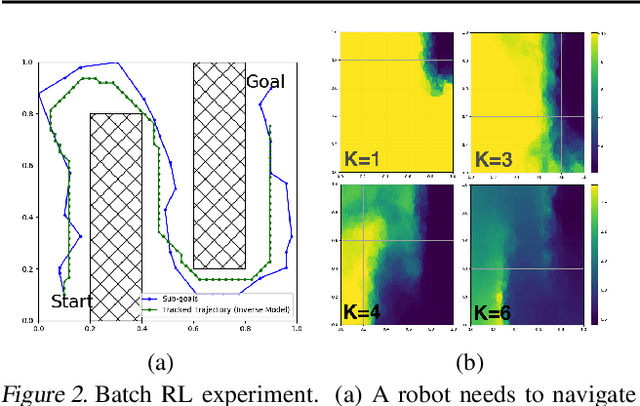

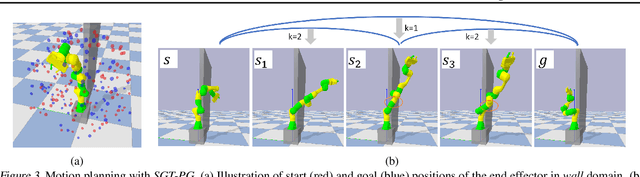
Many AI problems, in robotics and other domains, are goal-based, essentially seeking trajectories leading to various goal states. Reinforcement learning (RL), building on Bellman's optimality equation, naturally optimizes for a single goal, yet can be made multi-goal by augmenting the state with the goal. Instead, we propose a new RL framework, derived from a dynamic programming equation for the all pairs shortest path (APSP) problem, which naturally solves multi-goal queries. We show that this approach has computational benefits for both standard and approximate dynamic programming. Interestingly, our formulation prescribes a novel protocol for computing a trajectory: instead of predicting the next state given its predecessor, as in standard RL, a goal-conditioned trajectory is constructed by first predicting an intermediate state between start and goal, partitioning the trajectory into two. Then, recursively, predicting intermediate points on each sub-segment, until a complete trajectory is obtained. We call this trajectory structure a sub-goal tree. Building on it, we additionally extend the policy gradient methodology to recursively predict sub-goals, resulting in novel goal-based algorithms. Finally, we apply our method to neural motion planning, where we demonstrate significant improvements compared to standard RL on navigating a 7-DoF robot arm between obstacles.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge