Proceedings of the 2017 ICML Workshop on Human Interpretability in Machine Learning

This is the Proceedings of the 2017 ICML Workshop on Human Interpretability in Machine Learning (WHI 2017), which was held in Sydney, Australia, August 10, 2017. Invited speakers were Tony Jebara, Pang Wei Koh, and David Sontag.

Proceedings of the 2016 ICML Workshop on Human Interpretability in Machine Learning

This is the Proceedings of the 2016 ICML Workshop on Human Interpretability in Machine Learning (WHI 2016), which was held in New York, NY, June 23, 2016. Invited speakers were Susan Athey, Rich Caruana, Jacob Feldman, Percy Liang, and Hanna Wallach.

Interpretable Two-level Boolean Rule Learning for Classification

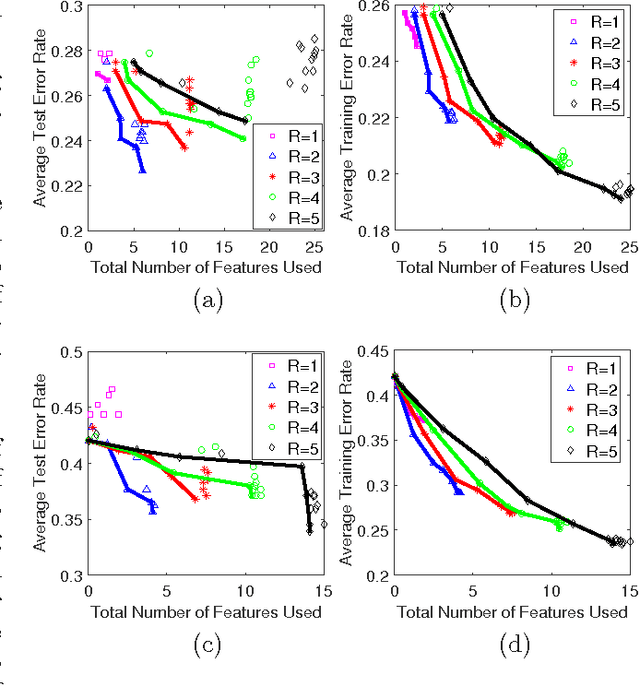
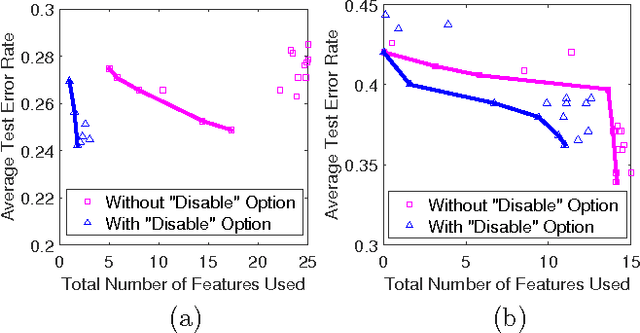
As a contribution to interpretable machine learning research, we develop a novel optimization framework for learning accurate and sparse two-level Boolean rules. We consider rules in both conjunctive normal form (AND-of-ORs) and disjunctive normal form (OR-of-ANDs). A principled objective function is proposed to trade classification accuracy and interpretability, where we use Hamming loss to characterize accuracy and sparsity to characterize interpretability. We propose efficient procedures to optimize these objectives based on linear programming (LP) relaxation, block coordinate descent, and alternating minimization. Experiments show that our new algorithms provide very good tradeoffs between accuracy and interpretability.

Lagrangian Relaxation for MAP Estimation in Graphical Models

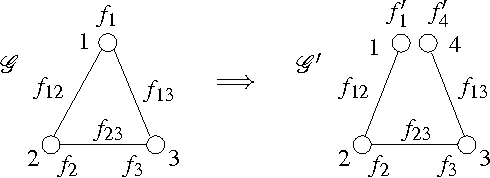
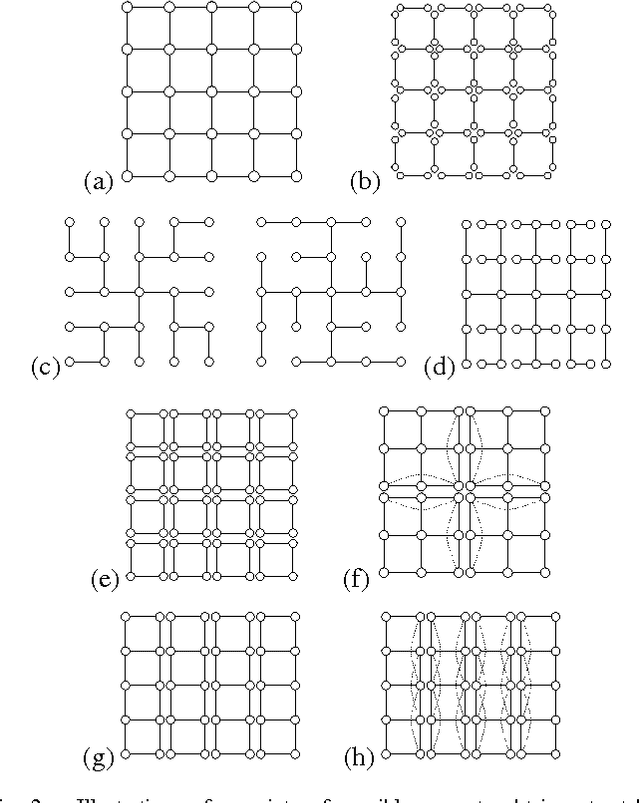
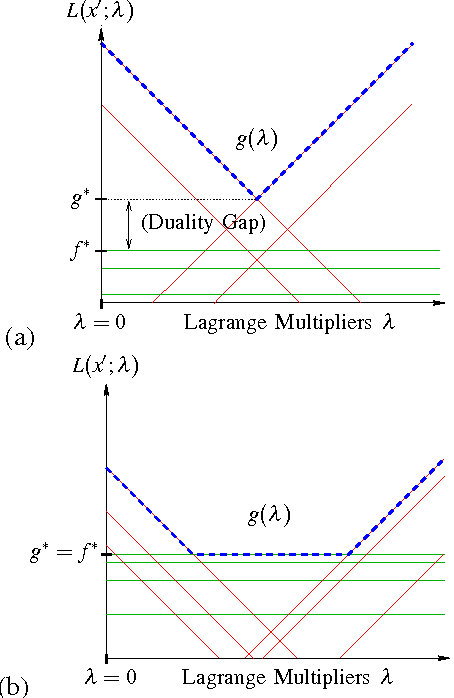
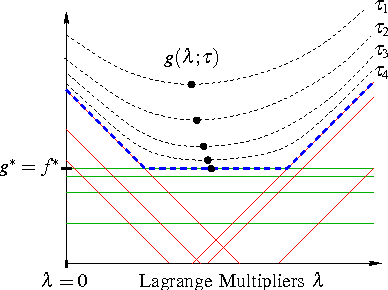
We develop a general framework for MAP estimation in discrete and Gaussian graphical models using Lagrangian relaxation techniques. The key idea is to reformulate an intractable estimation problem as one defined on a more tractable graph, but subject to additional constraints. Relaxing these constraints gives a tractable dual problem, one defined by a thin graph, which is then optimized by an iterative procedure. When this iterative optimization leads to a consistent estimate, one which also satisfies the constraints, then it corresponds to an optimal MAP estimate of the original model. Otherwise there is a ``duality gap'', and we obtain a bound on the optimal solution. Thus, our approach combines convex optimization with dynamic programming techniques applicable for thin graphs. The popular tree-reweighted max-product (TRMP) method may be seen as solving a particular class of such relaxations, where the intractable graph is relaxed to a set of spanning trees. We also consider relaxations to a set of small induced subgraphs, thin subgraphs (e.g. loops), and a connected tree obtained by ``unwinding'' cycles. In addition, we propose a new class of multiscale relaxations that introduce ``summary'' variables. The potential benefits of such generalizations include: reducing or eliminating the ``duality gap'' in hard problems, reducing the number or Lagrange multipliers in the dual problem, and accelerating convergence of the iterative optimization procedure.