Interpretable Two-level Boolean Rule Learning for Classification
Paper and Code
Jun 18, 2016
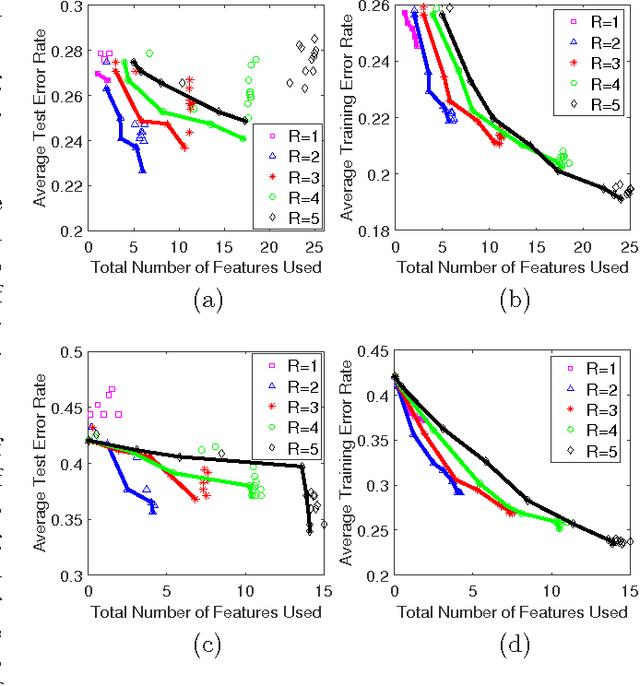

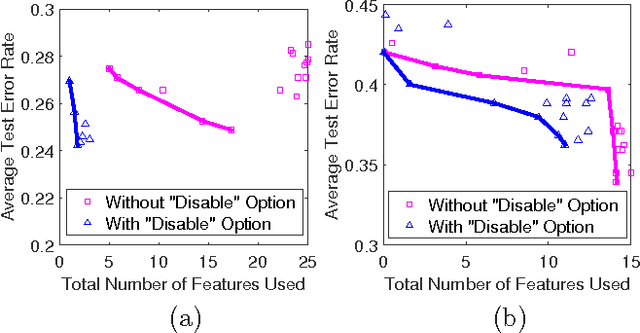
As a contribution to interpretable machine learning research, we develop a novel optimization framework for learning accurate and sparse two-level Boolean rules. We consider rules in both conjunctive normal form (AND-of-ORs) and disjunctive normal form (OR-of-ANDs). A principled objective function is proposed to trade classification accuracy and interpretability, where we use Hamming loss to characterize accuracy and sparsity to characterize interpretability. We propose efficient procedures to optimize these objectives based on linear programming (LP) relaxation, block coordinate descent, and alternating minimization. Experiments show that our new algorithms provide very good tradeoffs between accuracy and interpretability.
* presented at 2016 ICML Workshop on Human Interpretability in Machine
Learning (WHI 2016), New York, NY
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge