Lagrangian Relaxation for MAP Estimation in Graphical Models

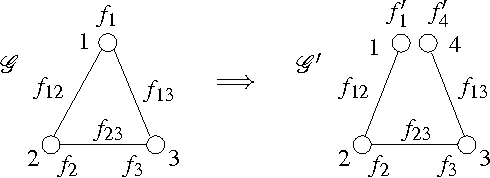
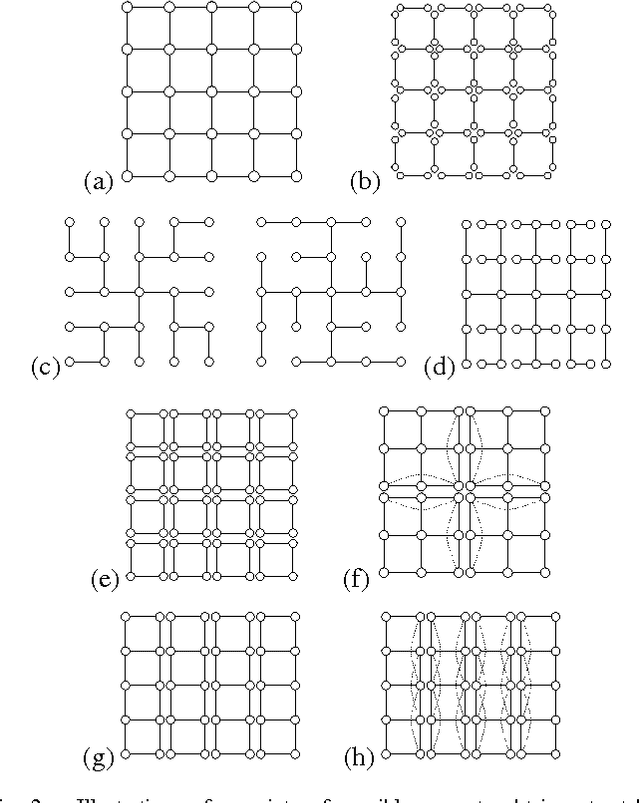
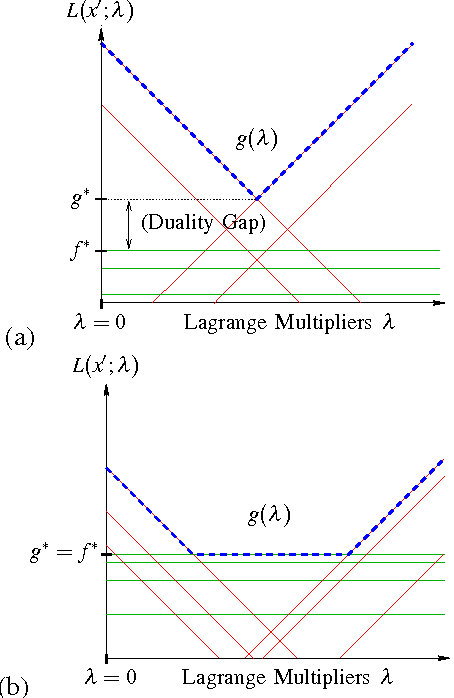
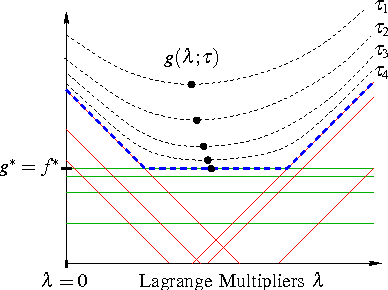
We develop a general framework for MAP estimation in discrete and Gaussian graphical models using Lagrangian relaxation techniques. The key idea is to reformulate an intractable estimation problem as one defined on a more tractable graph, but subject to additional constraints. Relaxing these constraints gives a tractable dual problem, one defined by a thin graph, which is then optimized by an iterative procedure. When this iterative optimization leads to a consistent estimate, one which also satisfies the constraints, then it corresponds to an optimal MAP estimate of the original model. Otherwise there is a ``duality gap'', and we obtain a bound on the optimal solution. Thus, our approach combines convex optimization with dynamic programming techniques applicable for thin graphs. The popular tree-reweighted max-product (TRMP) method may be seen as solving a particular class of such relaxations, where the intractable graph is relaxed to a set of spanning trees. We also consider relaxations to a set of small induced subgraphs, thin subgraphs (e.g. loops), and a connected tree obtained by ``unwinding'' cycles. In addition, we propose a new class of multiscale relaxations that introduce ``summary'' variables. The potential benefits of such generalizations include: reducing or eliminating the ``duality gap'' in hard problems, reducing the number or Lagrange multipliers in the dual problem, and accelerating convergence of the iterative optimization procedure.