Auto-GDA: Automatic Domain Adaptation for Efficient Grounding Verification in Retrieval Augmented Generation

While retrieval augmented generation (RAG) has been shown to enhance factuality of large language model (LLM) outputs, LLMs still suffer from hallucination, generating incorrect or irrelevant information. One common detection strategy involves prompting the LLM again to assess whether its response is grounded in the retrieved evidence, but this approach is costly. Alternatively, lightweight natural language inference (NLI) models for efficient grounding verification can be used at inference time. While existing pre-trained NLI models offer potential solutions, their performance remains subpar compared to larger models on realistic RAG inputs. RAG inputs are more complex than most datasets used for training NLI models and have characteristics specific to the underlying knowledge base, requiring adaptation of the NLI models to a specific target domain. Additionally, the lack of labeled instances in the target domain makes supervised domain adaptation, e.g., through fine-tuning, infeasible. To address these challenges, we introduce Automatic Generative Domain Adaptation (Auto-GDA). Our framework enables unsupervised domain adaptation through synthetic data generation. Unlike previous methods that rely on handcrafted filtering and augmentation strategies, Auto-GDA employs an iterative process to continuously improve the quality of generated samples using weak labels from less efficient teacher models and discrete optimization to select the most promising augmented samples. Experimental results demonstrate the effectiveness of our approach, with models fine-tuned on synthetic data using Auto-GDA often surpassing the performance of the teacher model and reaching the performance level of LLMs at 10 % of their computational cost.

On the Usefulness of Synthetic Tabular Data Generation

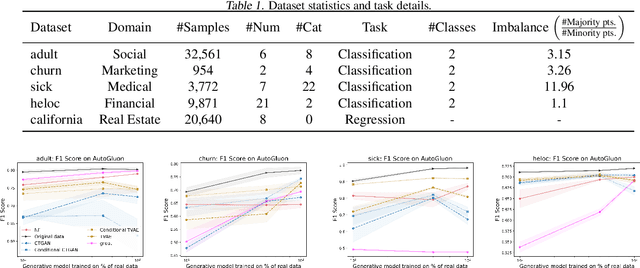
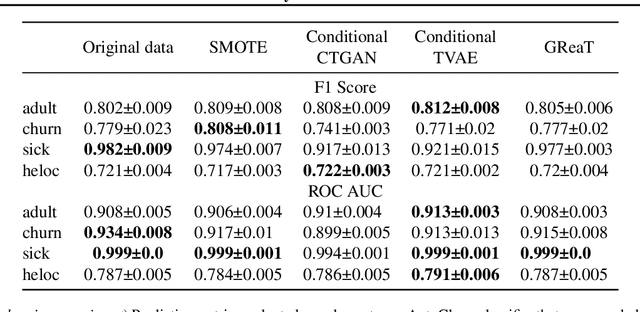
Despite recent advances in synthetic data generation, the scientific community still lacks a unified consensus on its usefulness. It is commonly believed that synthetic data can be used for both data exchange and boosting machine learning (ML) training. Privacy-preserving synthetic data generation can accelerate data exchange for downstream tasks, but there is not enough evidence to show how or why synthetic data can boost ML training. In this study, we benchmarked ML performance using synthetic tabular data for four use cases: data sharing, data augmentation, class balancing, and data summarization. We observed marginal improvements for the balancing use case on some datasets. However, we conclude that there is not enough evidence to claim that synthetic tabular data is useful for ML training.

Black-box Coreset Variational Inference

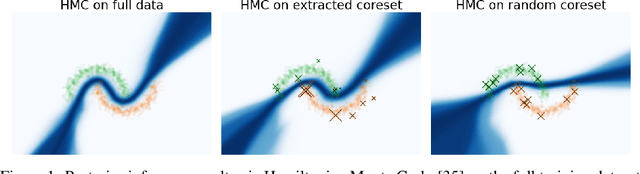
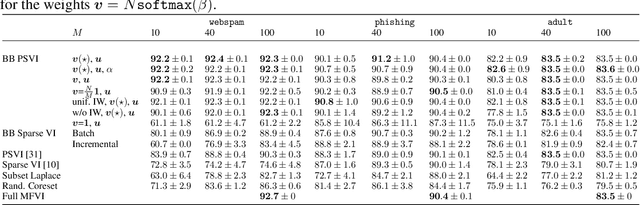
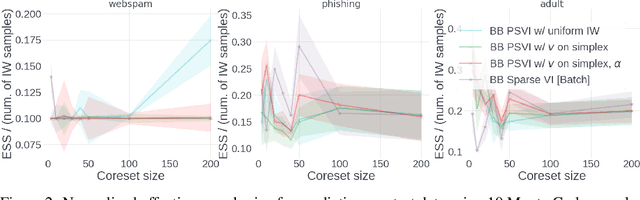
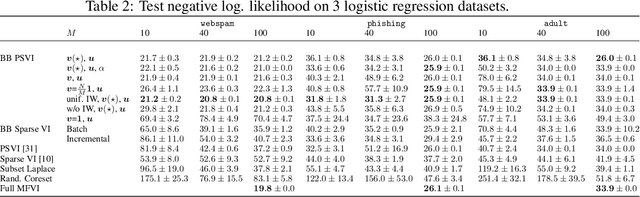
Recent advances in coreset methods have shown that a selection of representative datapoints can replace massive volumes of data for Bayesian inference, preserving the relevant statistical information and significantly accelerating subsequent downstream tasks. Existing variational coreset constructions rely on either selecting subsets of the observed datapoints, or jointly performing approximate inference and optimizing pseudodata in the observed space akin to inducing points methods in Gaussian Processes. So far, both approaches are limited by complexities in evaluating their objectives for general purpose models, and require generating samples from a typically intractable posterior over the coreset throughout inference and testing. In this work, we present a black-box variational inference framework for coresets that overcomes these constraints and enables principled application of variational coresets to intractable models, such as Bayesian neural networks. We apply our techniques to supervised learning problems, and compare them with existing approaches in the literature for data summarization and inference.

$β$-Cores: Robust Large-Scale Bayesian Data Summarization in the Presence of Outliers

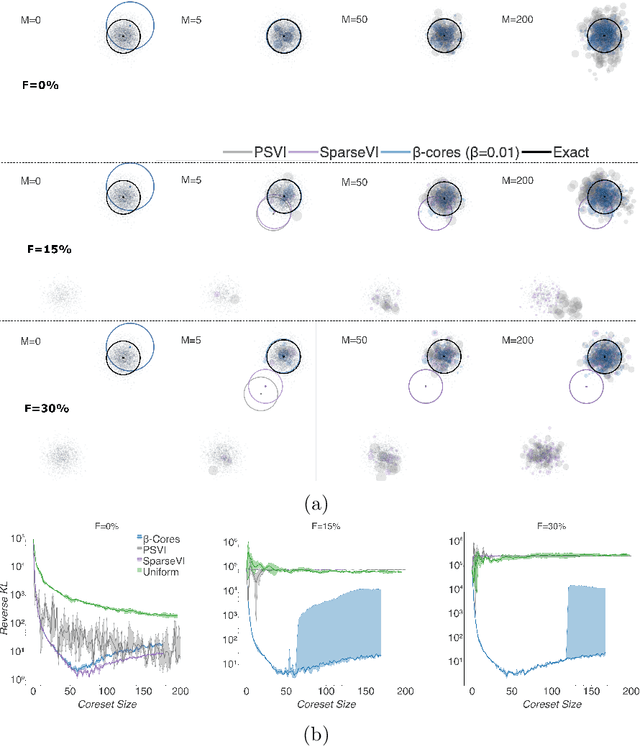
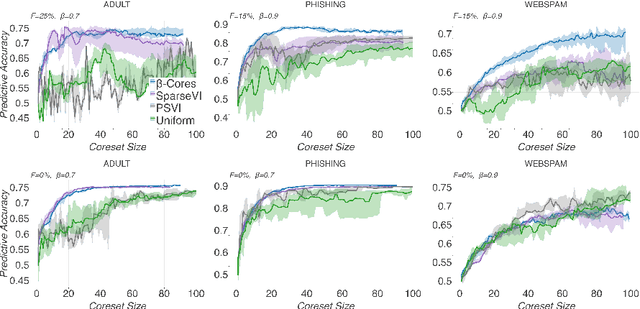
Modern machine learning applications should be able to address the intrinsic challenges arising over inference on massive real-world datasets, including scalability and robustness to outliers. Despite the multiple benefits of Bayesian methods (such as uncertainty-aware predictions, incorporation of experts knowledge, and hierarchical modeling), the quality of classic Bayesian inference depends critically on whether observations conform with the assumed data generating model, which is impossible to guarantee in practice. In this work, we propose a variational inference method that, in a principled way, can simultaneously scale to large datasets, and robustify the inferred posterior with respect to the existence of outliers in the observed data. Reformulating Bayes theorem via the $\beta$-divergence, we posit a robustified pseudo-Bayesian posterior as the target of inference. Moreover, relying on the recent formulations of Riemannian coresets for scalable Bayesian inference, we propose a sparse variational approximation of the robustified posterior and an efficient stochastic black-box algorithm to construct it. Overall our method allows releasing cleansed data summaries that can be applied broadly in scenarios including structured data corruption. We illustrate the applicability of our approach in diverse simulated and real datasets, and various statistical models, including Gaussian mean inference, logistic and neural linear regression, demonstrating its superiority to existing Bayesian summarization methods in the presence of outliers.