Black-box Coreset Variational Inference

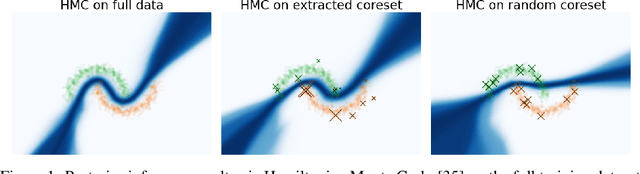
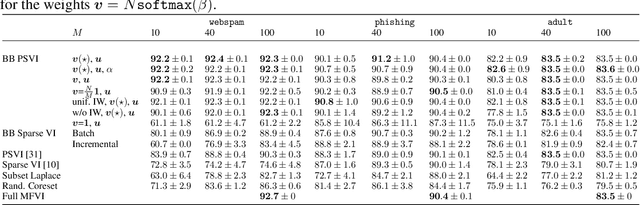
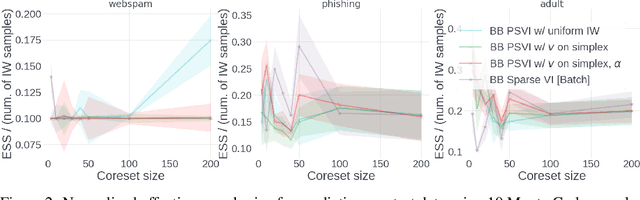
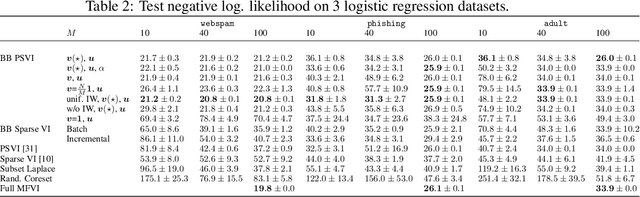
Recent advances in coreset methods have shown that a selection of representative datapoints can replace massive volumes of data for Bayesian inference, preserving the relevant statistical information and significantly accelerating subsequent downstream tasks. Existing variational coreset constructions rely on either selecting subsets of the observed datapoints, or jointly performing approximate inference and optimizing pseudodata in the observed space akin to inducing points methods in Gaussian Processes. So far, both approaches are limited by complexities in evaluating their objectives for general purpose models, and require generating samples from a typically intractable posterior over the coreset throughout inference and testing. In this work, we present a black-box variational inference framework for coresets that overcomes these constraints and enables principled application of variational coresets to intractable models, such as Bayesian neural networks. We apply our techniques to supervised learning problems, and compare them with existing approaches in the literature for data summarization and inference.

TyXe: Pyro-based Bayesian neural nets for Pytorch

We introduce TyXe, a Bayesian neural network library built on top of Pytorch and Pyro. Our leading design principle is to cleanly separate architecture, prior, inference and likelihood specification, allowing for a flexible workflow where users can quickly iterate over combinations of these components. In contrast to existing packages TyXe does not implement any layer classes, and instead relies on architectures defined in generic Pytorch code. TyXe then provides modular choices for canonical priors, variational guides, inference techniques, and layer selections for a Bayesian treatment of the specified architecture. Sampling tricks for variance reduction, such as local reparameterization or flipout, are implemented as effect handlers, which can be applied independently of other specifications. We showcase the ease of use of TyXe to explore Bayesian versions of popular models from various libraries: toy regression with a pure Pytorch neural network; large-scale image classification with torchvision ResNets; graph neural networks based on DGL; and Neural Radiance Fields built on top of Pytorch3D. Finally, we provide convenient abstractions for variational continual learning. In all cases the change from a deterministic to a Bayesian neural network comes with minimal modifications to existing code, offering a broad range of researchers and practitioners alike practical access to uncertainty estimation techniques. The library is available at https://github.com/TyXe-BDL/TyXe.

Sparse Uncertainty Representation in Deep Learning with Inducing Weights

Bayesian neural networks and deep ensembles represent two modern paradigms of uncertainty quantification in deep learning. Yet these approaches struggle to scale mainly due to memory inefficiency issues, since they require parameter storage several times higher than their deterministic counterparts. To address this, we augment the weight matrix of each layer with a small number of inducing weights, thereby projecting the uncertainty quantification into such low dimensional spaces. We further extend Matheron's conditional Gaussian sampling rule to enable fast weight sampling, which enables our inference method to maintain reasonable run-time as compared with ensembles. Importantly, our approach achieves competitive performance to the state-of-the-art in prediction and uncertainty estimation tasks with fully connected neural networks and ResNets, while reducing the parameter size to $\leq 24.3\%$ of that of a $single$ neural network.

Bayesian Online Meta-Learning with Laplace Approximation

Neural networks are known to suffer from catastrophic forgetting when trained on sequential datasets. While there have been numerous attempts to solve this problem for large-scale supervised classification, little has been done to overcome catastrophic forgetting for few-shot classification problems. We demonstrate that the popular gradient-based few-shot meta-learning algorithm Model-Agnostic Meta-Learning (MAML) indeed suffers from catastrophic forgetting and introduce a Bayesian online meta-learning framework that tackles this problem. Our framework incorporates MAML into a Bayesian online learning algorithm with Laplace approximation. This framework enables few-shot classification on a range of sequentially arriving datasets with a single meta-learned model. The experimental evaluations demonstrate that our framework can effectively prevent forgetting in various few-shot classification settings compared to applying MAML sequentially.

Gaussian Mean Field Regularizes by Limiting Learned Information

Variational inference with a factorized Gaussian posterior estimate is a widely used approach for learning parameters and hidden variables. Empirically, a regularizing effect can be observed that is poorly understood. In this work, we show how mean field inference improves generalization by limiting mutual information between learned parameters and the data through noise. We quantify a maximum capacity when the posterior variance is either fixed or learned and connect it to generalization error, even when the KL-divergence in the objective is rescaled. Our experiments demonstrate that bounding information between parameters and data effectively regularizes neural networks on both supervised and unsupervised tasks.

Online Structured Laplace Approximations For Overcoming Catastrophic Forgetting

We introduce the Kronecker factored online Laplace approximation for overcoming catastrophic forgetting in neural networks. The method is grounded in a Bayesian online learning framework, where we recursively approximate the posterior after every task with a Gaussian, leading to a quadratic penalty on changes to the weights. The Laplace approximation requires calculating the Hessian around a mode, which is typically intractable for modern architectures. In order to make our method scalable, we leverage recent block-diagonal Kronecker factored approximations to the curvature. Our algorithm achieves over 90% test accuracy across a sequence of 50 instantiations of the permuted MNIST dataset, substantially outperforming related methods for overcoming catastrophic forgetting.

Practical Gauss-Newton Optimisation for Deep Learning

We present an efficient block-diagonal ap- proximation to the Gauss-Newton matrix for feedforward neural networks. Our result- ing algorithm is competitive against state- of-the-art first order optimisation methods, with sometimes significant improvement in optimisation performance. Unlike first-order methods, for which hyperparameter tuning of the optimisation parameters is often a labo- rious process, our approach can provide good performance even when used with default set- tings. A side result of our work is that for piecewise linear transfer functions, the net- work objective function can have no differ- entiable local maxima, which may partially explain why such transfer functions facilitate effective optimisation.