GraphSAC: Detecting anomalies in large-scale graphs

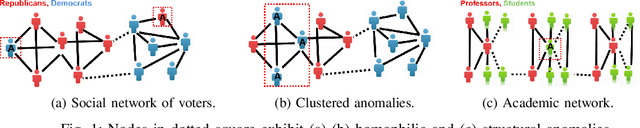
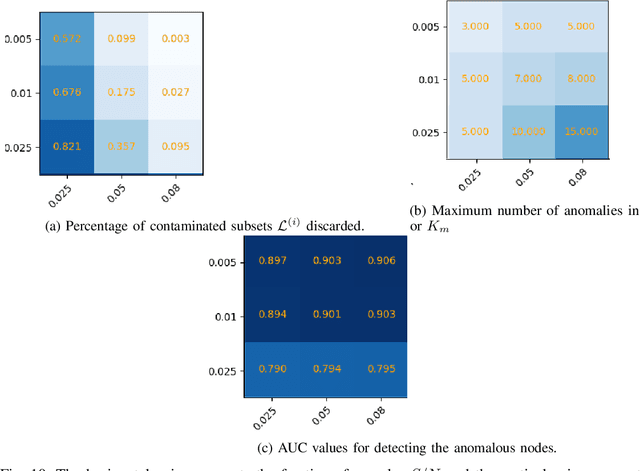
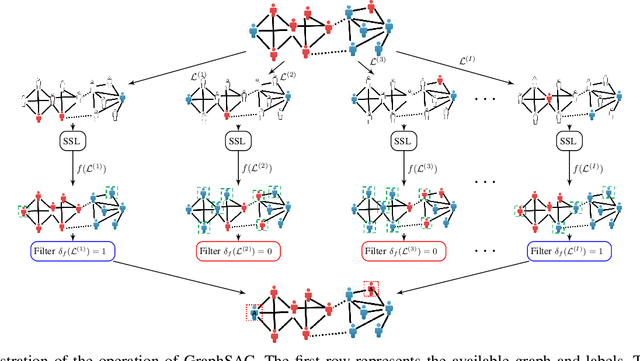
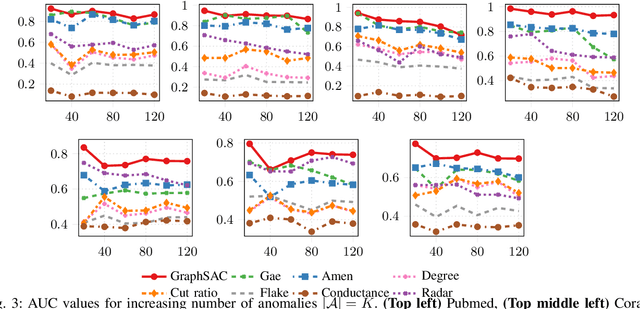
A graph-based sampling and consensus (GraphSAC) approach is introduced to effectively detect anomalous nodes in large-scale graphs. Existing approaches rely on connectivity and attributes of all nodes to assign an anomaly score per node. However, nodal attributes and network links might be compromised by adversaries, rendering these holistic approaches vulnerable. Alleviating this limitation, GraphSAC randomly draws subsets of nodes, and relies on graph-aware criteria to judiciously filter out sets contaminated by anomalous nodes, before employing a semi-supervised learning (SSL) module to estimate nominal label distributions per node. These learned nominal distributions are minimally affected by the anomalous nodes, and hence can be directly adopted for anomaly detection. Rigorous analysis provides performance guarantees for GraphSAC, by bounding the required number of draws. The per-draw complexity grows linearly with the number of edges, which implies efficient SSL, while draws can be run in parallel, thereby ensuring scalability to large graphs. GraphSAC is tested under different anomaly generation models based on random walks, clustered anomalies, as well as contemporary adversarial attacks for graph data. Experiments with real-world graphs showcase the advantage of GraphSAC relative to state-of-the-art alternatives.

Node Embedding with Adaptive Similarities for Scalable Learning over Graphs

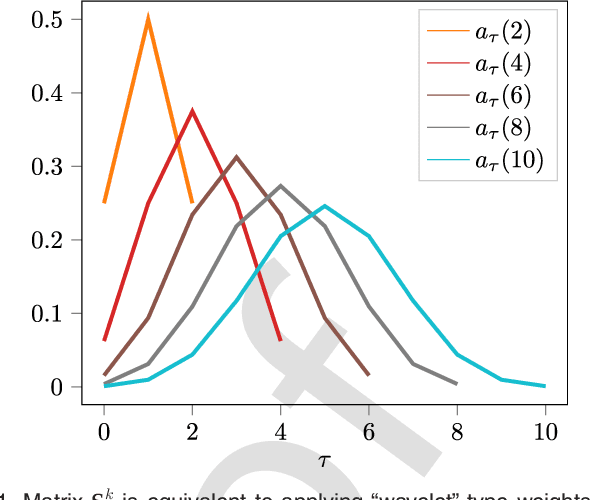
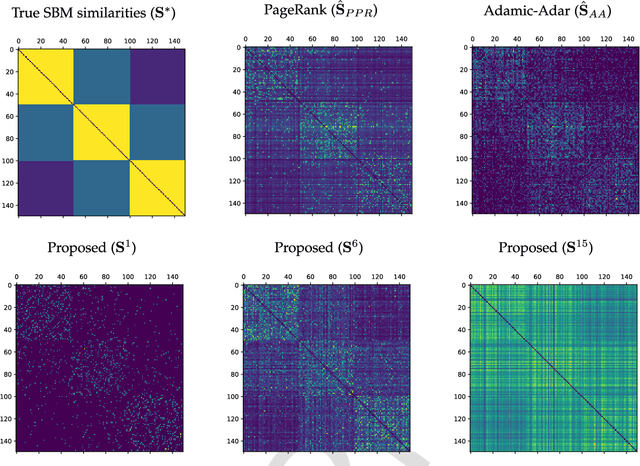
Node embedding is the task of extracting informative and descriptive features over the nodes of a graph. The importance of node embeddings for graph analytics, as well as learning tasks such as node classification, link prediction and community detection, has led to increased interest on the problem leading to a number of recent advances. Much like PCA in the feature domain, node embedding is an inherently \emph{unsupervised} task; in lack of metadata used for validation, practical methods may require standardization and limiting the use of tunable hyperparameters. Finally, node embedding methods are faced with maintaining scalability in the face of large-scale real-world graphs of ever-increasing sizes. In the present work, we propose an adaptive node embedding framework that adjusts the embedding process to a given underlying graph, in a fully unsupervised manner. To achieve this, we adopt the notion of a tunable node similarity matrix that assigns weights on paths of different length. The design of the multilength similarities ensures that the resulting embeddings also inherit interpretable spectral properties. The proposed model is carefully studied, interpreted, and numerically evaluated using stochastic block models. Moreover, an algorithmic scheme is proposed for training the model parameters effieciently and in an unsupervised manner. We perform extensive node classification, link prediction, and clustering experiments on many real world graphs from various domains, and compare with state-of-the-art scalable and unsupervised node embedding alternatives. The proposed method enjoys superior performance in many cases, while also yielding interpretable information on the underlying structure of the graph.

Adaptive Diffusions for Scalable Learning over Graphs

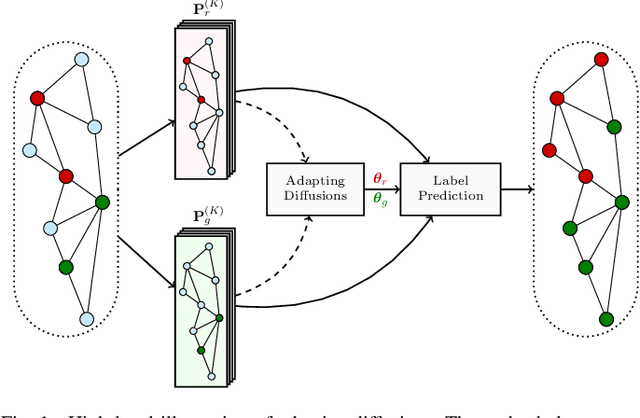
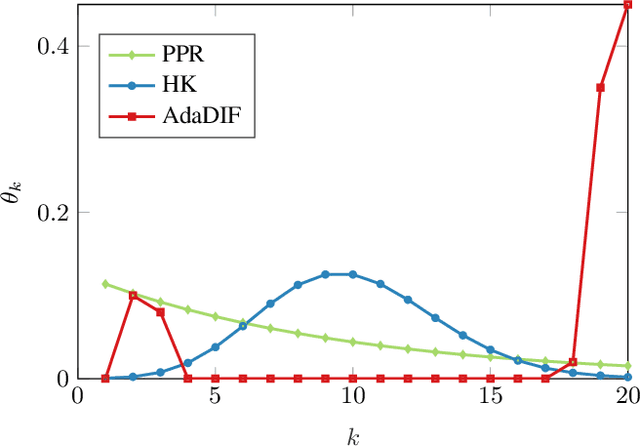
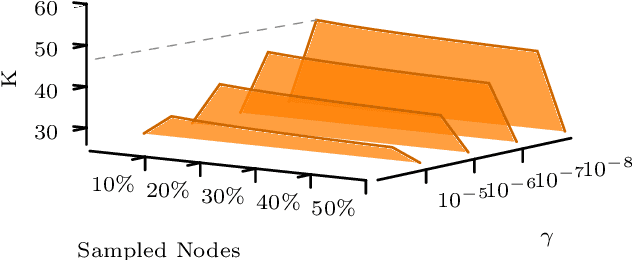
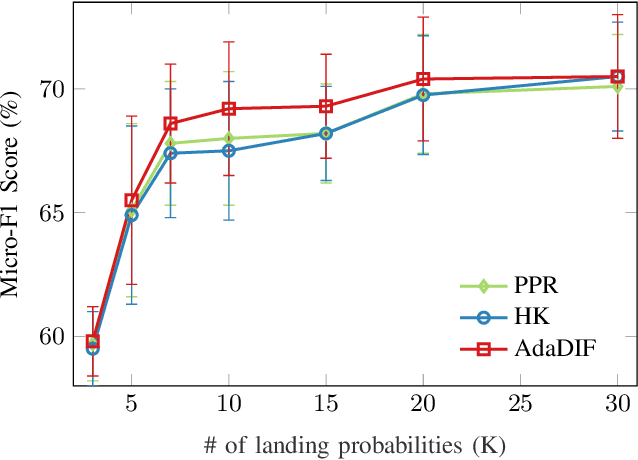
Diffusion-based classifiers such as those relying on the Personalized PageRank and the Heat kernel, enjoy remarkable classification accuracy at modest computational requirements. Their performance however is affected by the extent to which the chosen diffusion captures a typically unknown label propagation mechanism, that can be specific to the underlying graph, and potentially different for each class. The present work introduces a disciplined, data-efficient approach to learning class-specific diffusion functions adapted to the underlying network topology. The novel learning approach leverages the notion of "landing probabilities" of class-specific random walks, which can be computed efficiently, thereby ensuring scalability to large graphs. This is supported by rigorous analysis of the properties of the model as well as the proposed algorithms. Furthermore, a robust version of the classifier facilitates learning even in noisy environments. Classification tests on real networks demonstrate that adapting the diffusion function to the given graph and observed labels, significantly improves the performance over fixed diffusions; reaching -- and many times surpassing -- the classification accuracy of computationally heavier state-of-the-art competing methods, that rely on node embeddings and deep neural networks.

Data-adaptive Active Sampling for Efficient Graph-Cognizant Classification

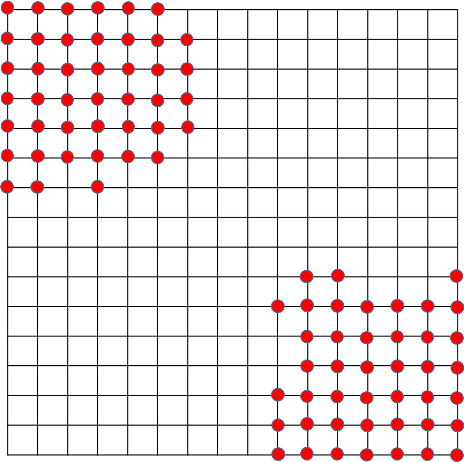
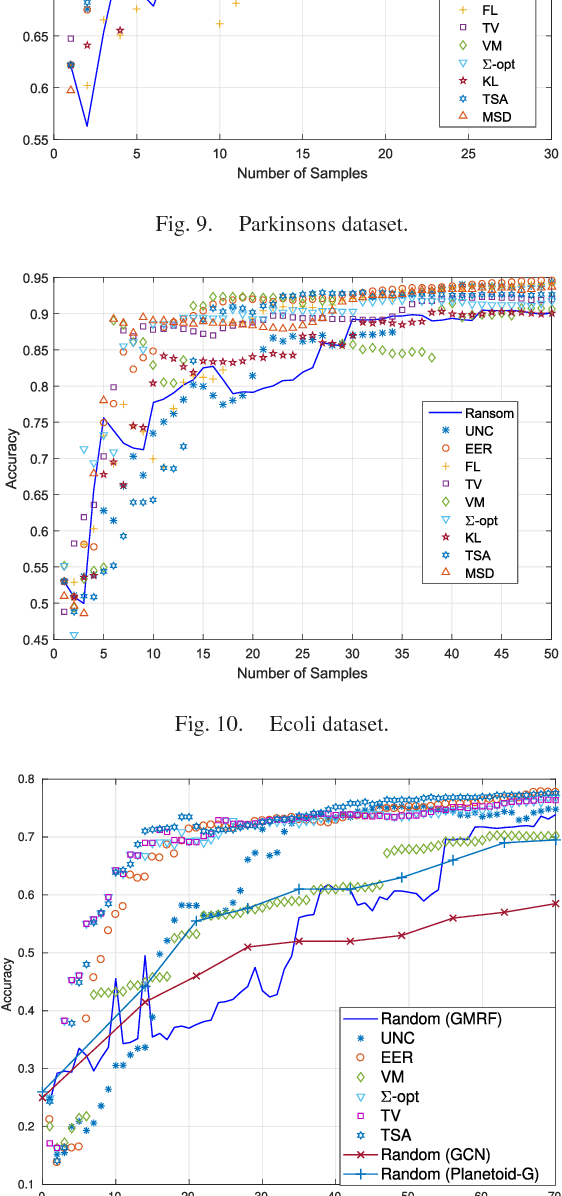
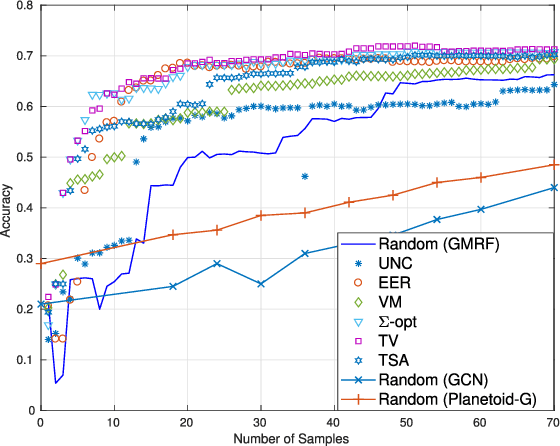
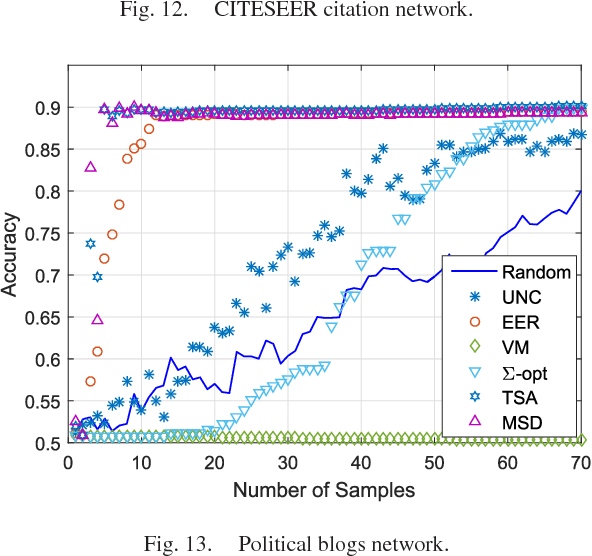
The present work deals with active sampling of graph nodes representing training data for binary classification. The graph may be given or constructed using similarity measures among nodal features. Leveraging the graph for classification builds on the premise that labels across neighboring nodes are correlated according to a categorical Markov random field (MRF). This model is further relaxed to a Gaussian (G)MRF with labels taking continuous values - an approximation that not only mitigates the combinatorial complexity of the categorical model, but also offers optimal unbiased soft predictors of the unlabeled nodes. The proposed sampling strategy is based on querying the node whose label disclosure is expected to inflict the largest change on the GMRF, and in this sense it is the most informative on average. Such a strategy subsumes several measures of expected model change, including uncertainty sampling, variance minimization, and sampling based on the $\Sigma-$optimality criterion. A simple yet effective heuristic is also introduced for increasing the exploration capabilities of the sampler, and reducing bias of the resultant classifier, by taking into account the confidence on the model label predictions. The novel sampling strategies are based on quantities that are readily available without the need for model retraining, rendering them computationally efficient and scalable to large graphs. Numerical tests using synthetic and real data demonstrate that the proposed methods achieve accuracy that is comparable or superior to the state-of-the-art even at reduced runtime.

Large-scale Kernel-based Feature Extraction via Budgeted Nonlinear Subspace Tracking

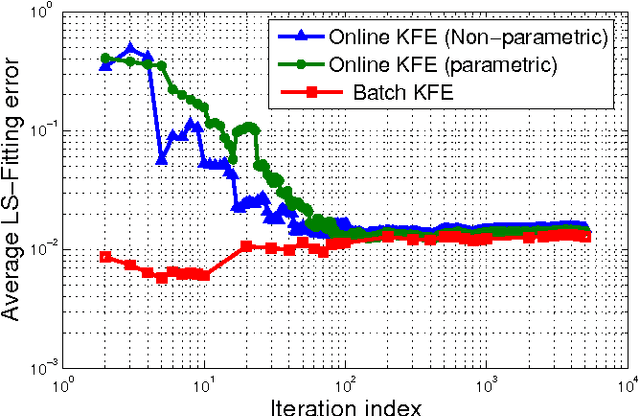
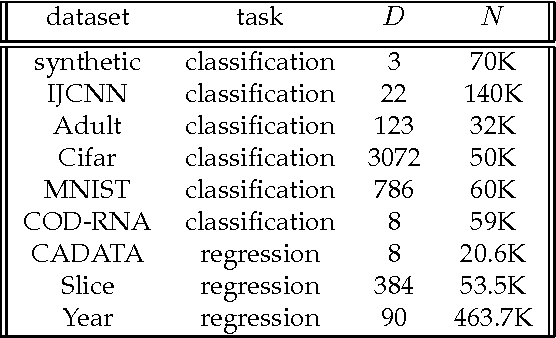
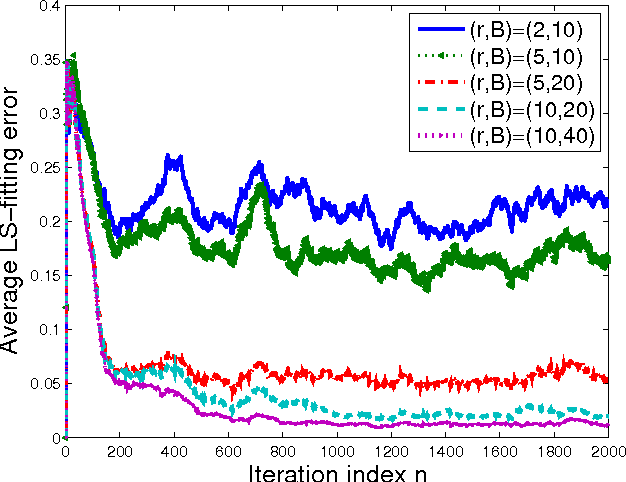
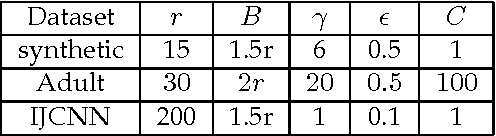
Kernel-based methods enjoy powerful generalization capabilities in handling a variety of learning tasks. When such methods are provided with sufficient training data, broadly-applicable classes of nonlinear functions can be approximated with desired accuracy. Nevertheless, inherent to the nonparametric nature of kernel-based estimators are computational and memory requirements that become prohibitive with large-scale datasets. In response to this formidable challenge, the present work puts forward a low-rank, kernel-based, feature extraction approach that is particularly tailored for online operation, where data streams need not be stored in memory. A novel generative model is introduced to approximate high-dimensional (possibly infinite) features via a low-rank nonlinear subspace, the learning of which leads to a direct kernel function approximation. Offline and online solvers are developed for the subspace learning task, along with affordable versions, in which the number of stored data vectors is confined to a predefined budget. Analytical results provide performance bounds on how well the kernel matrix as well as kernel-based classification and regression tasks can be approximated by leveraging budgeted online subspace learning and feature extraction schemes. Tests on synthetic and real datasets demonstrate and benchmark the efficiency of the proposed method when linear classification and regression is applied to the extracted features.

Online Censoring for Large-Scale Regressions with Application to Streaming Big Data

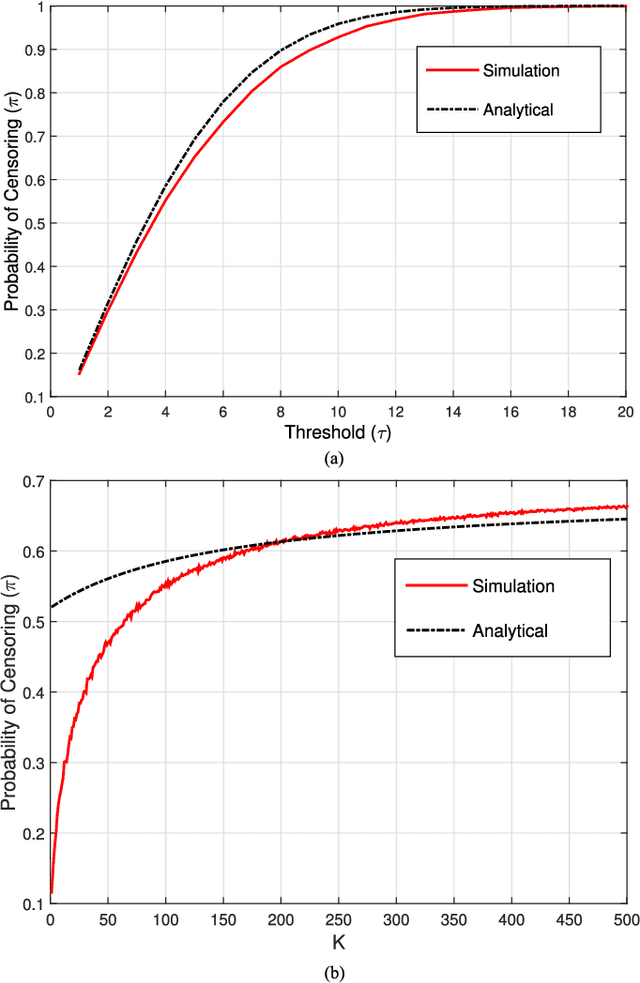
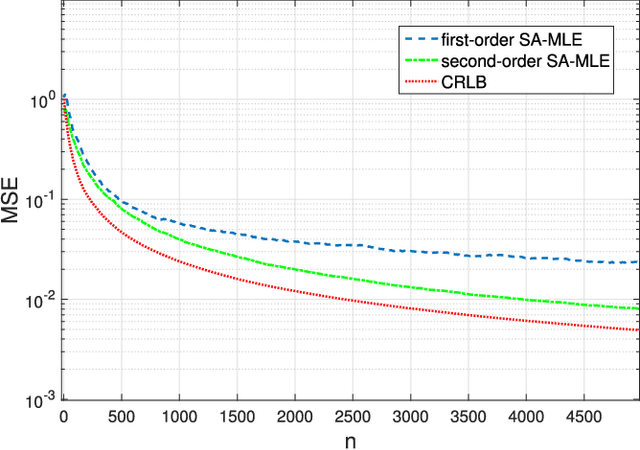
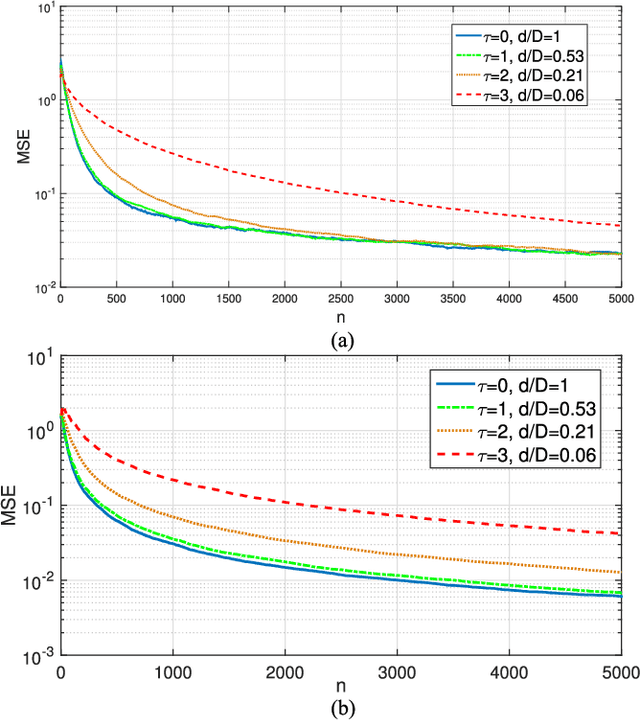
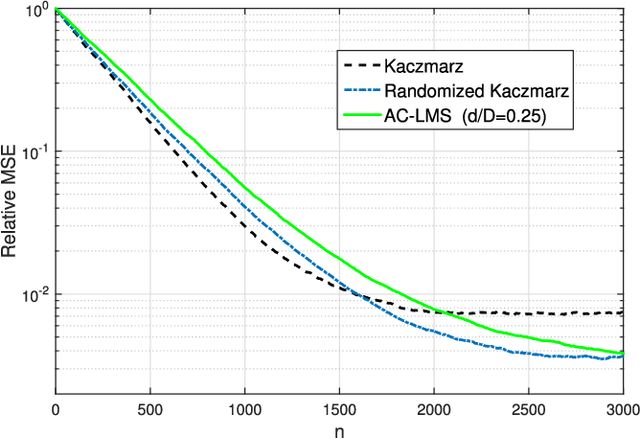
Linear regression is arguably the most prominent among statistical inference methods, popular both for its simplicity as well as its broad applicability. On par with data-intensive applications, the sheer size of linear regression problems creates an ever growing demand for quick and cost efficient solvers. Fortunately, a significant percentage of the data accrued can be omitted while maintaining a certain quality of statistical inference with an affordable computational budget. The present paper introduces means of identifying and omitting "less informative" observations in an online and data-adaptive fashion, built on principles of stochastic approximation and data censoring. First- and second-order stochastic approximation maximum likelihood-based algorithms for censored observations are developed for estimating the regression coefficients. Online algorithms are also put forth to reduce the overall complexity by adaptively performing censoring along with estimation. The novel algorithms entail simple closed-form updates, and have provable (non)asymptotic convergence guarantees. Furthermore, specific rules are investigated for tuning to desired censoring patterns and levels of dimensionality reduction. Simulated tests on real and synthetic datasets corroborate the efficacy of the proposed data-adaptive methods compared to data-agnostic random projection-based alternatives.