Online Censoring for Large-Scale Regressions with Application to Streaming Big Data
Paper and Code
Jul 27, 2015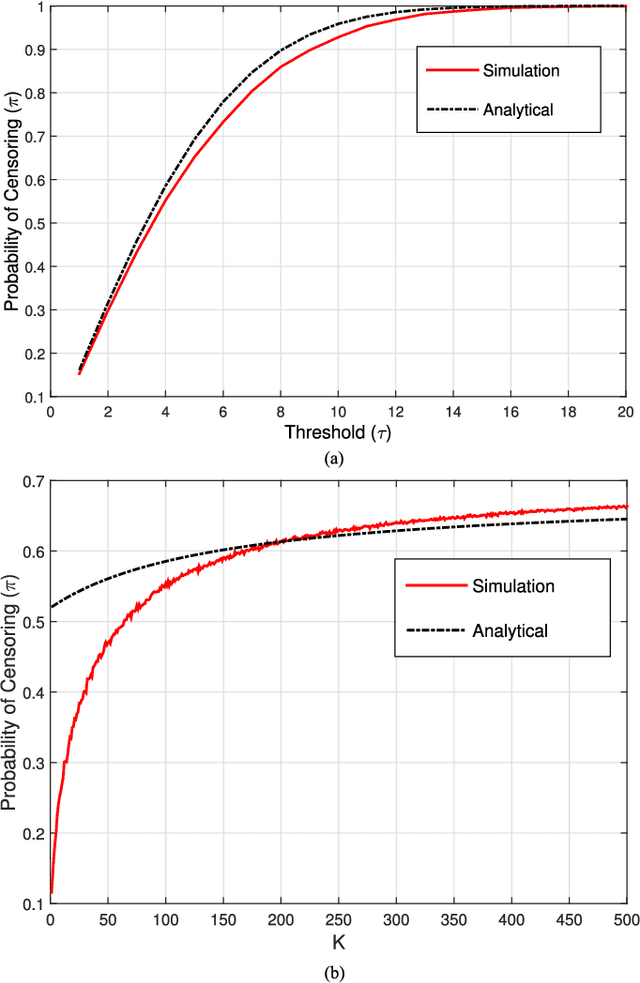
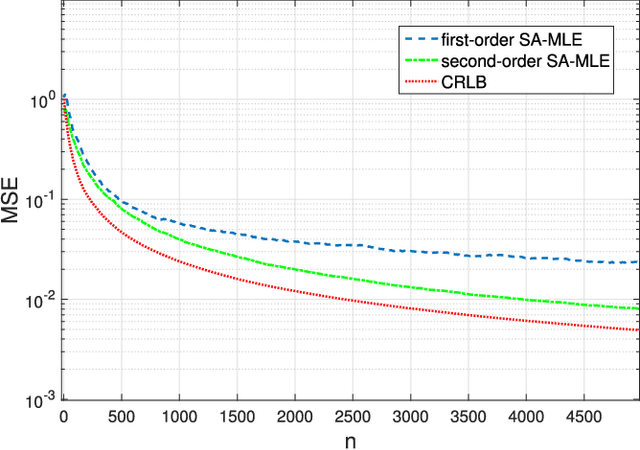
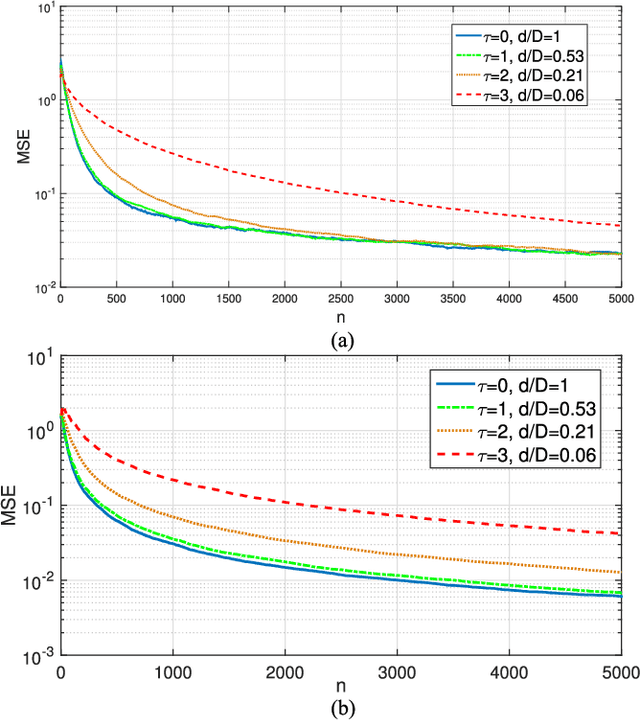
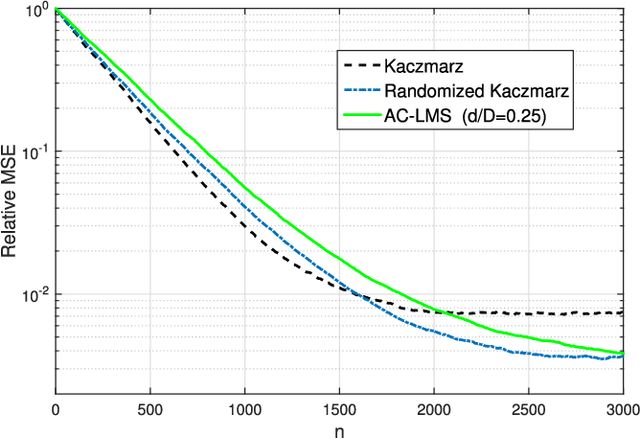
Linear regression is arguably the most prominent among statistical inference methods, popular both for its simplicity as well as its broad applicability. On par with data-intensive applications, the sheer size of linear regression problems creates an ever growing demand for quick and cost efficient solvers. Fortunately, a significant percentage of the data accrued can be omitted while maintaining a certain quality of statistical inference with an affordable computational budget. The present paper introduces means of identifying and omitting "less informative" observations in an online and data-adaptive fashion, built on principles of stochastic approximation and data censoring. First- and second-order stochastic approximation maximum likelihood-based algorithms for censored observations are developed for estimating the regression coefficients. Online algorithms are also put forth to reduce the overall complexity by adaptively performing censoring along with estimation. The novel algorithms entail simple closed-form updates, and have provable (non)asymptotic convergence guarantees. Furthermore, specific rules are investigated for tuning to desired censoring patterns and levels of dimensionality reduction. Simulated tests on real and synthetic datasets corroborate the efficacy of the proposed data-adaptive methods compared to data-agnostic random projection-based alternatives.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge