Large-scale Kernel-based Feature Extraction via Budgeted Nonlinear Subspace Tracking

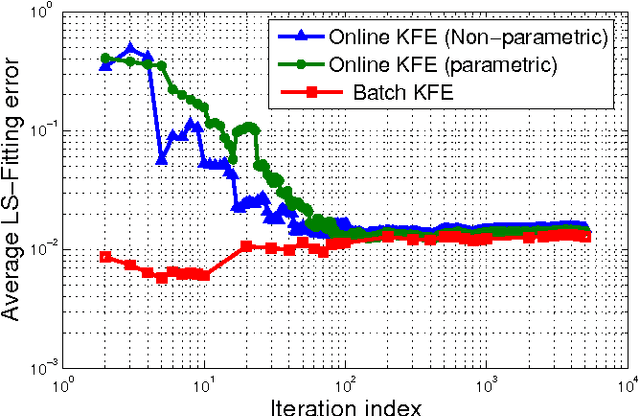
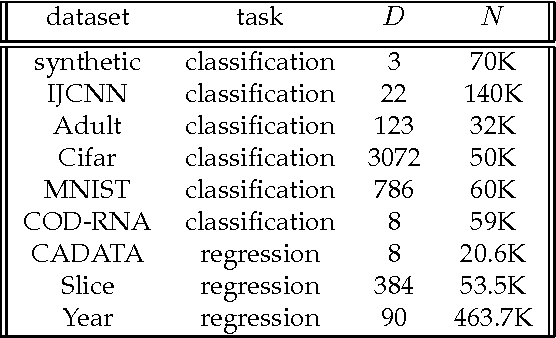
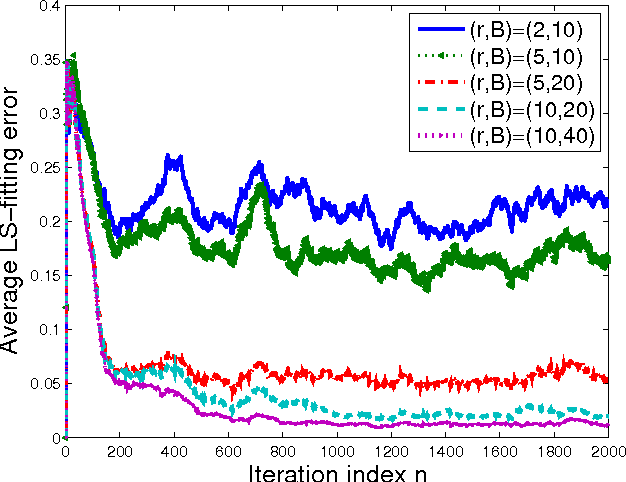
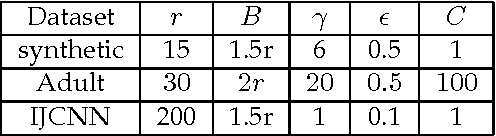
Kernel-based methods enjoy powerful generalization capabilities in handling a variety of learning tasks. When such methods are provided with sufficient training data, broadly-applicable classes of nonlinear functions can be approximated with desired accuracy. Nevertheless, inherent to the nonparametric nature of kernel-based estimators are computational and memory requirements that become prohibitive with large-scale datasets. In response to this formidable challenge, the present work puts forward a low-rank, kernel-based, feature extraction approach that is particularly tailored for online operation, where data streams need not be stored in memory. A novel generative model is introduced to approximate high-dimensional (possibly infinite) features via a low-rank nonlinear subspace, the learning of which leads to a direct kernel function approximation. Offline and online solvers are developed for the subspace learning task, along with affordable versions, in which the number of stored data vectors is confined to a predefined budget. Analytical results provide performance bounds on how well the kernel matrix as well as kernel-based classification and regression tasks can be approximated by leveraging budgeted online subspace learning and feature extraction schemes. Tests on synthetic and real datasets demonstrate and benchmark the efficiency of the proposed method when linear classification and regression is applied to the extracted features.