Data-adaptive Active Sampling for Efficient Graph-Cognizant Classification
Paper and Code
Dec 26, 2017
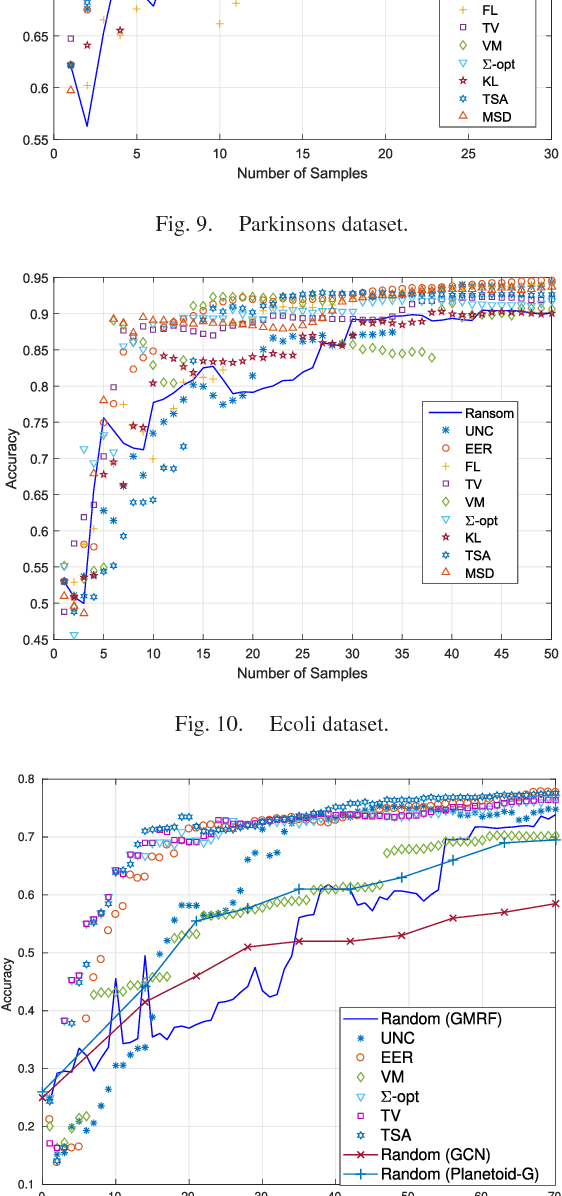
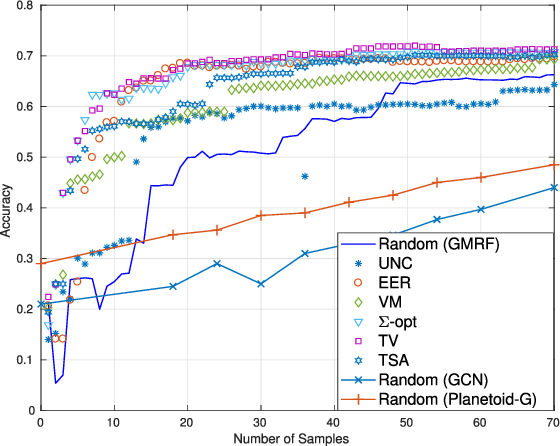
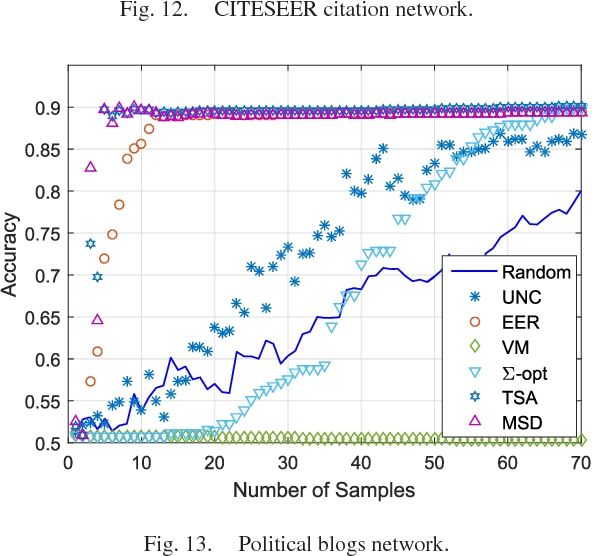
The present work deals with active sampling of graph nodes representing training data for binary classification. The graph may be given or constructed using similarity measures among nodal features. Leveraging the graph for classification builds on the premise that labels across neighboring nodes are correlated according to a categorical Markov random field (MRF). This model is further relaxed to a Gaussian (G)MRF with labels taking continuous values - an approximation that not only mitigates the combinatorial complexity of the categorical model, but also offers optimal unbiased soft predictors of the unlabeled nodes. The proposed sampling strategy is based on querying the node whose label disclosure is expected to inflict the largest change on the GMRF, and in this sense it is the most informative on average. Such a strategy subsumes several measures of expected model change, including uncertainty sampling, variance minimization, and sampling based on the $\Sigma-$optimality criterion. A simple yet effective heuristic is also introduced for increasing the exploration capabilities of the sampler, and reducing bias of the resultant classifier, by taking into account the confidence on the model label predictions. The novel sampling strategies are based on quantities that are readily available without the need for model retraining, rendering them computationally efficient and scalable to large graphs. Numerical tests using synthetic and real data demonstrate that the proposed methods achieve accuracy that is comparable or superior to the state-of-the-art even at reduced runtime.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge