Tensor Ring Optimized Quantum-Enhanced Tensor Neural Networks

Quantum machine learning researchers often rely on incorporating Tensor Networks (TN) into Deep Neural Networks (DNN) and variational optimization. However, the standard optimization techniques used for training the contracted trainable weights of each model layer suffer from the correlations and entanglement structure between the model parameters on classical implementations. To address this issue, a multi-layer design of a Tensor Ring optimized variational Quantum learning classifier (Quan-TR) comprising cascading entangling gates replacing the fully connected (dense) layers of a TN is proposed, and it is referred to as Tensor Ring optimized Quantum-enhanced tensor neural Networks (TR-QNet). TR-QNet parameters are optimized through the stochastic gradient descent algorithm on qubit measurements. The proposed TR-QNet is assessed on three distinct datasets, namely Iris, MNIST, and CIFAR-10, to demonstrate the enhanced precision achieved for binary classification. On quantum simulations, the proposed TR-QNet achieves promising accuracy of $94.5\%$, $86.16\%$, and $83.54\%$ on the Iris, MNIST, and CIFAR-10 datasets, respectively. Benchmark studies have been conducted on state-of-the-art quantum and classical implementations of TN models to show the efficacy of the proposed TR-QNet. Moreover, the scalability of TR-QNet highlights its potential for exhibiting in deep learning applications on a large scale. The PyTorch implementation of TR-QNet is available on Github:https://github.com/konar1987/TR-QNet/

Noisy Tensor Ring approximation for computing gradients of Variational Quantum Eigensolver for Combinatorial Optimization

Variational Quantum algorithms, especially Quantum Approximate Optimization and Variational Quantum Eigensolver (VQE) have established their potential to provide computational advantage in the realm of combinatorial optimization. However, these algorithms suffer from classically intractable gradients limiting the scalability. This work addresses the scalability challenge for VQE by proposing a classical gradient computation method which utilizes the parameter shift rule but computes the expected values from the circuits using a tensor ring approximation. The parametrized gates from the circuit transform the tensor ring by contracting the matrix along the free edges of the tensor ring. While the single qubit gates do not alter the ring structure, the state transformations from the two qubit rotations are evaluated by truncating the singular values thereby preserving the structure of the tensor ring and reducing the computational complexity. This variation of the Matrix product state approximation grows linearly in number of qubits and the number of two qubit gates as opposed to the exponential growth in the classical simulations, allowing for a faster evaluation of the gradients on classical simulators.

Tensor Ring Parametrized Variational Quantum Circuits for Large Scale Quantum Machine Learning

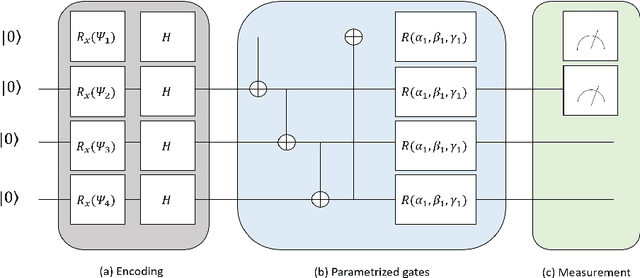
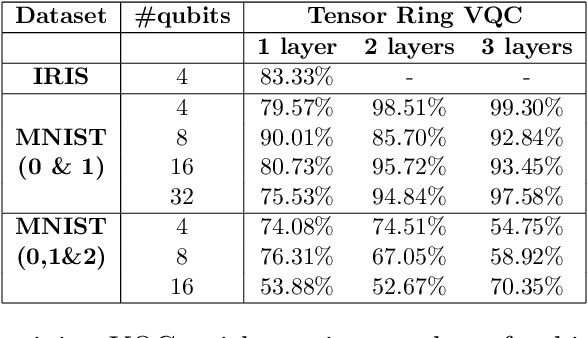
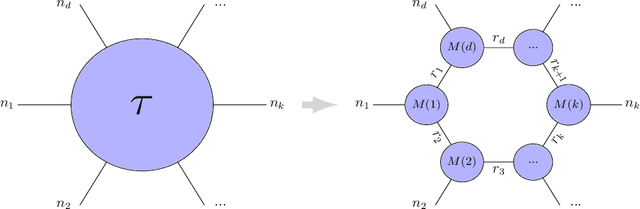
Quantum Machine Learning (QML) is an emerging research area advocating the use of quantum computing for advancement in machine learning. Since the discovery of the capability of Parametrized Variational Quantum Circuits (VQC) to replace Artificial Neural Networks, they have been widely adopted to different tasks in Quantum Machine Learning. However, despite their potential to outperform neural networks, VQCs are limited to small scale applications given the challenges in scalability of quantum circuits. To address this shortcoming, we propose an algorithm that compresses the quantum state within the circuit using a tensor ring representation. Using the input qubit state in the tensor ring representation, single qubit gates maintain the tensor ring representation. However, the same is not true for two qubit gates in general, where an approximation is used to have the output as a tensor ring representation. Using this approximation, the storage and computational time increases linearly in the number of qubits and number of layers, as compared to the exponential increase with exact simulation algorithms. This approximation is used to implement the tensor ring VQC. The training of the parameters of tensor ring VQC is performed using a gradient descent based algorithm, where efficient approaches for backpropagation are used. The proposed approach is evaluated on two datasets: Iris and MNIST for the classification task to show the improved accuracy using more number of qubits. We achieve a test accuracy of 83.33\% on Iris dataset and a maximum of 99.30\% and 76.31\% on binary and ternary classification of MNIST dataset using various circuit architectures. The results from the IRIS dataset outperform the results on VQC implemented on Qiskit, and being scalable, demonstrates the potential for VQCs to be used for large scale Quantum Machine Learning applications.

An FEA surrogate model with Boundary Oriented Graph Embedding approach

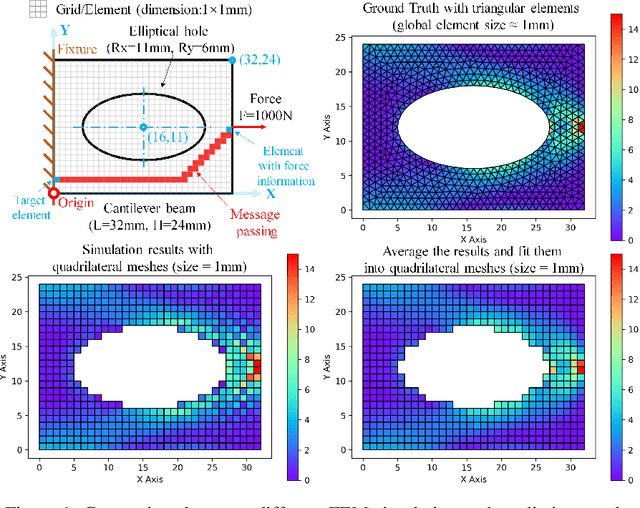
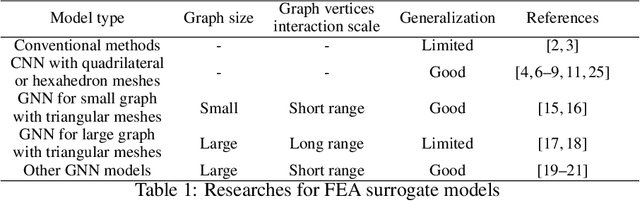
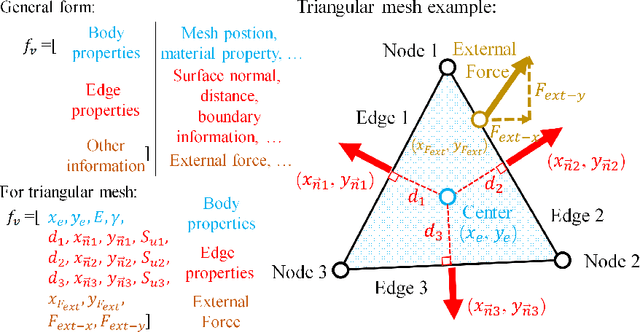
In this work, we present a Boundary Oriented Graph Embedding (BOGE) approach for the Graph Neural Network (GNN) to serve as a general surrogate model for regressing physical fields and solving boundary value problems. Providing shortcuts for both boundary elements and local neighbor elements, the BOGE approach can embed structured mesh elements into the graph and performs an efficient regression on large-scale triangular-mesh-based FEA results, which cannot be realized by other machine-learning-based surrogate methods. Focusing on the cantilever beam problem, our BOGE approach cannot only fit the distribution of stress fields but also regresses the topological optimization results, which show its potential of realizing abstract decision-making design process. The BOGE approach with 3-layer DeepGCN model \textcolor{blue}{achieves the regression with MSE of 0.011706 (2.41\% MAPE) for stress field prediction and 0.002735 MSE (with 1.58\% elements having error larger than 0.01) for topological optimization.} The overall concept of the BOGE approach paves the way for a general and efficient deep-learning-based FEA simulator that will benefit both industry and design-related areas.

Efficient Gaussian Process Bandits by Believing only Informative Actions

Bayesian optimization is a framework for global search via maximum a posteriori updates rather than simulated annealing, and has gained prominence for decision-making under uncertainty. In this work, we cast Bayesian optimization as a multi-armed bandit problem, where the payoff function is sampled from a Gaussian process (GP). Further, we focus on action selections via upper confidence bound (UCB) or expected improvement (EI) due to their prevalent use in practice. Prior works using GPs for bandits cannot allow the iteration horizon $T$ to be large, as the complexity of computing the posterior parameters scales cubically with the number of past observations. To circumvent this computational burden, we propose a simple statistical test: only incorporate an action into the GP posterior when its conditional entropy exceeds an $\epsilon$ threshold. Doing so permits us to derive sublinear regret bounds of GP bandit algorithms up to factors depending on the compression parameter $\epsilon$ for both discrete and continuous action sets. Moreover, the complexity of the GP posterior remains provably finite. Experimentally, we observe state of the art accuracy and complexity tradeoffs for GP bandit algorithms applied to global optimization, suggesting the merits of compressed GPs in bandit settings.