An Optimal Hybrid Variance-Reduced Algorithm for Stochastic Composite Nonconvex Optimization

In this note we propose a new variant of the hybrid variance-reduced proximal gradient method in [7] to solve a common stochastic composite nonconvex optimization problem under standard assumptions. We simply replace the independent unbiased estimator in our hybrid- SARAH estimator introduced in [7] by the stochastic gradient evaluated at the same sample, leading to the identical momentum-SARAH estimator introduced in [2]. This allows us to save one stochastic gradient per iteration compared to [7], and only requires two samples per iteration. Our algorithm is very simple and achieves optimal stochastic oracle complexity bound in terms of stochastic gradient evaluations (up to a constant factor). Our analysis is essentially inspired by [7], but we do not use two different step-sizes.

Robust and Generalizable Visual Representation Learning via Random Convolutions

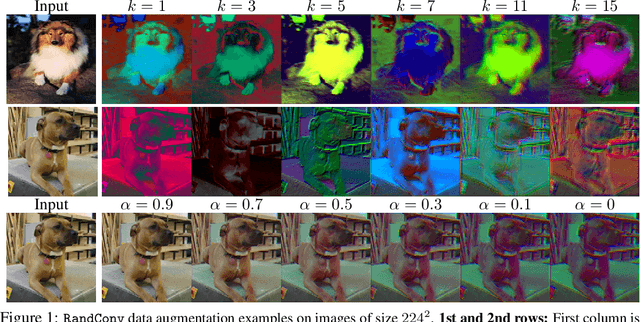
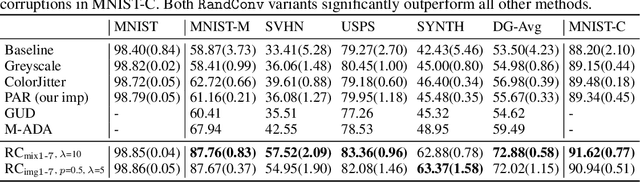
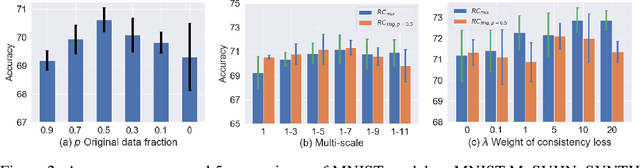
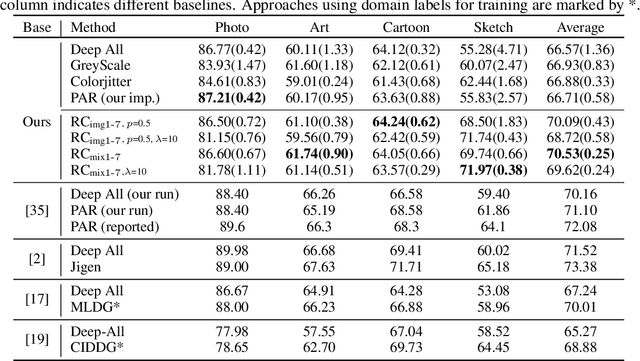
While successful for various computer vision tasks, deep neural networks have shown to be vulnerable to texture style shifts and small perturbations to which humans are robust. Hence, our goal is to train models in such a way that improves their robustness to these perturbations. We are motivated by the approximately shape-preserving property of randomized convolutions, which is due to distance preservation under random linear transforms. Intuitively, randomized convolutions create an infinite number of new domains with similar object shapes but random local texture. Therefore, we explore using outputs of multi-scale random convolutions as new images or mixing them with the original images during training. When applying a network trained with our approach to unseen domains, our method consistently improves the performance on domain generalization benchmarks and is scalable to ImageNet. Especially for the challenging scenario of generalizing to the sketch domain in PACS and to ImageNet-Sketch, our method outperforms state-of-art methods by a large margin. More interestingly, our method can benefit downstream tasks by providing a more robust pretrained visual representation.

Hybrid Variance-Reduced SGD Algorithms For Nonconvex-Concave Minimax Problems

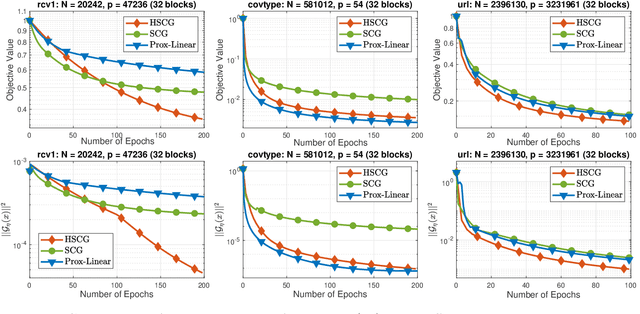
We develop a novel variance-reduced algorithm to solve a stochastic nonconvex-concave minimax problem which has various applications in different fields. This problem has several computational challenges due to its nonsmoothness, nonconvexity, nonlinearity, and non-separability of the objective functions. Our approach relies on a novel combination of recent ideas, including smoothing and hybrid stochastic variance-reduced techniques. Our algorithm and its variants can achieve $\mathcal{O}(T^{-2/3})$-convergence rate in $T$, and the best-known oracle complexity under standard assumptions. They have several computational advantages compared to existing methods. They can also work with both single sample or mini-batch on derivative estimators, with constant or diminishing step-sizes. We demonstrate the benefits of our algorithms over existing methods through two numerical examples.

Randomized Primal-Dual Algorithms for Composite Convex Minimization with Faster Convergence Rates

We develop two novel randomized primal-dual algorithms to solve nonsmooth composite convex optimization problems. The first algorithm is fully randomized, i.e., it has randomized updates on both primal and dual variables, while the second one is a semi-randomized scheme which only has one randomized update on the primal (or dual) variable while using the full update for the other. Both algorithms achieve the best-known $\mathcal{O}(1/k)$ or $\mathcal{O}(1/k^2)$ convergence rates in expectation under either only convexity or strong convexity, respectively, where $k$ is the iteration counter. Interestingly, with new parameter update rules, our algorithms can achieve $o(1/k)$ or $o(1/k^2)$ best-iterate convergence rate in expectation under either convexity or strong convexity, respectively. These rates can be obtained for both the primal and dual problems. To the best of our knowledge, this is the first time such faster convergence rates are shown for randomized primal-dual methods. Finally, we verify our theoretical results via two numerical examples and compare them with the state-of-the-art.

A Newton Frank-Wolfe Method for Constrained Self-Concordant Minimization

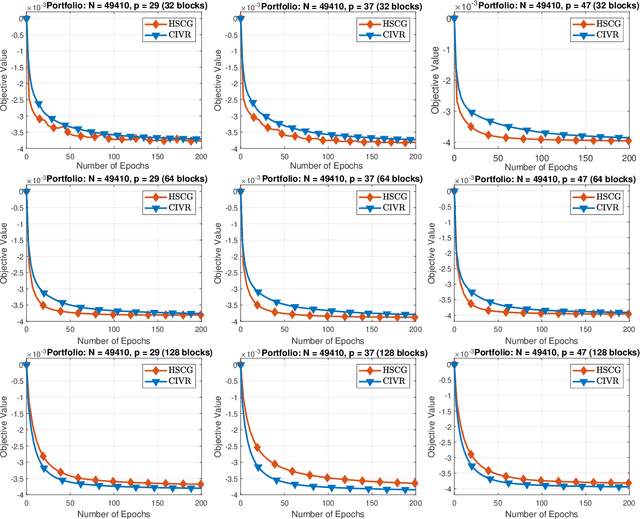
We demonstrate how to scalably solve a class of constrained self-concordant minimization problems using linear minimization oracles (LMO) over the constraint set. We prove that the number of LMO calls of our method is nearly the same as that of the Frank-Wolfe method in the L-smooth case. Specifically, our Newton Frank-Wolfe method uses $\mathcal{O}(\epsilon^{-\nu})$ LMO's, where $\epsilon$ is the desired accuracy and $\nu:= 1 + o(1)$. In addition, we demonstrate how our algorithm can exploit the improved variants of the LMO-based schemes, including away-steps, to attain linear convergence rates. We also provide numerical evidence with portfolio design with the competitive ratio, D-optimal experimental design, and logistic regression with the elastic net where Newton Frank-Wolfe outperforms the state-of-the-art.