Hybrid Variance-Reduced SGD Algorithms For Nonconvex-Concave Minimax Problems

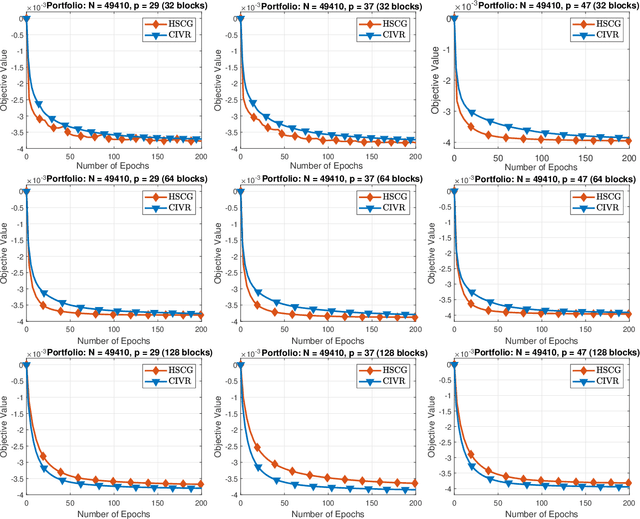
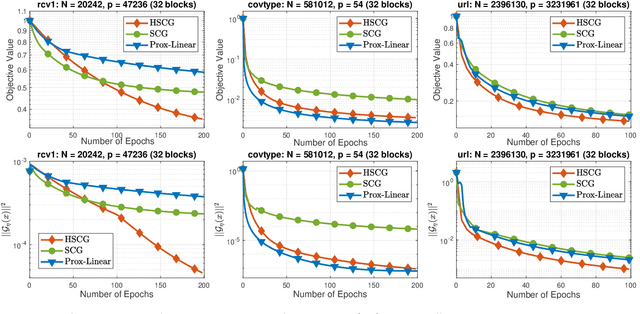
We develop a novel variance-reduced algorithm to solve a stochastic nonconvex-concave minimax problem which has various applications in different fields. This problem has several computational challenges due to its nonsmoothness, nonconvexity, nonlinearity, and non-separability of the objective functions. Our approach relies on a novel combination of recent ideas, including smoothing and hybrid stochastic variance-reduced techniques. Our algorithm and its variants can achieve $\mathcal{O}(T^{-2/3})$-convergence rate in $T$, and the best-known oracle complexity under standard assumptions. They have several computational advantages compared to existing methods. They can also work with both single sample or mini-batch on derivative estimators, with constant or diminishing step-sizes. We demonstrate the benefits of our algorithms over existing methods through two numerical examples.