Randomized Primal-Dual Algorithms for Composite Convex Minimization with Faster Convergence Rates

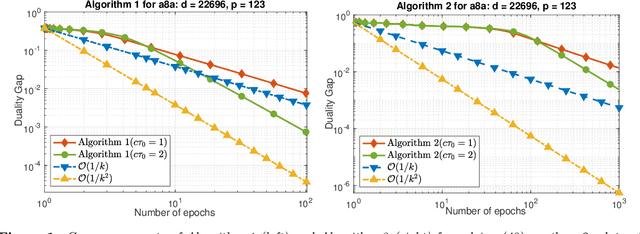
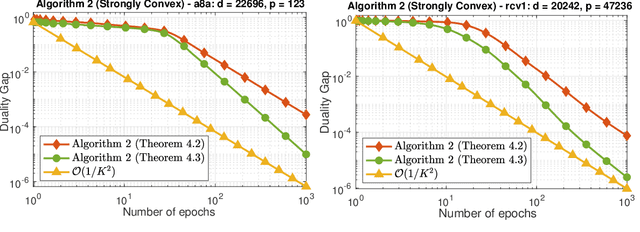
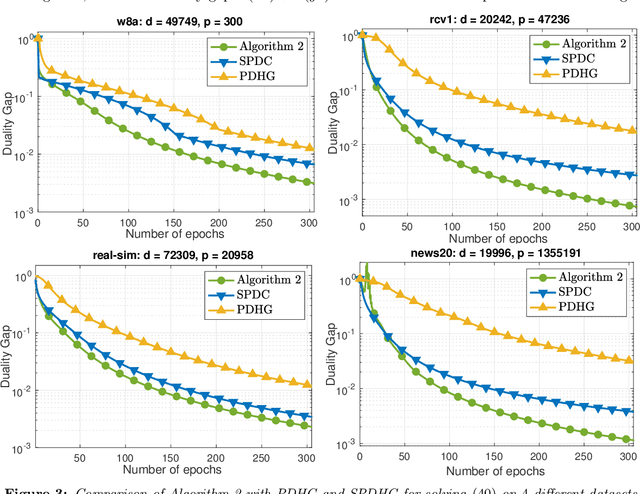
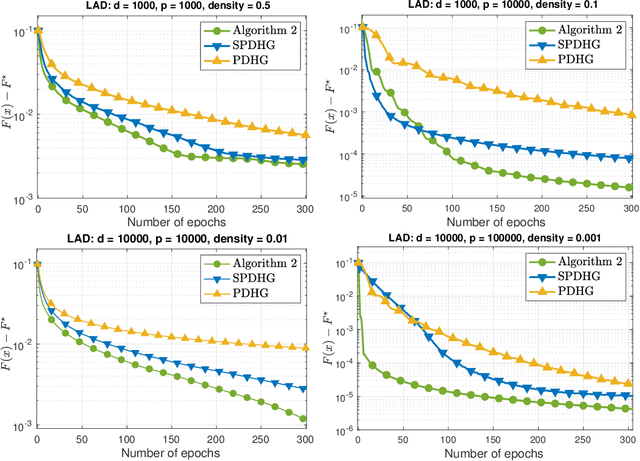
We develop two novel randomized primal-dual algorithms to solve nonsmooth composite convex optimization problems. The first algorithm is fully randomized, i.e., it has randomized updates on both primal and dual variables, while the second one is a semi-randomized scheme which only has one randomized update on the primal (or dual) variable while using the full update for the other. Both algorithms achieve the best-known $\mathcal{O}(1/k)$ or $\mathcal{O}(1/k^2)$ convergence rates in expectation under either only convexity or strong convexity, respectively, where $k$ is the iteration counter. Interestingly, with new parameter update rules, our algorithms can achieve $o(1/k)$ or $o(1/k^2)$ best-iterate convergence rate in expectation under either convexity or strong convexity, respectively. These rates can be obtained for both the primal and dual problems. To the best of our knowledge, this is the first time such faster convergence rates are shown for randomized primal-dual methods. Finally, we verify our theoretical results via two numerical examples and compare them with the state-of-the-art.